题目内容
已知a∈R,函数f(x)=2x2(x-a).
(1)求函数f(x)在区间[1,2]上最小值h(a);
(2)对(1)中的h(a),若关于a的方程h(a)=k(a+1)有两个不同的实数解,求实数k的取值范围;
(3)若点A(a1,h(a1)),B(a2,h(a2)),C(a3,h(a3)),从左到右依次是函数y=h(a)图象上三点,且这三点不共线,求证:△ABC是钝角三角形.
(1)求函数f(x)在区间[1,2]上最小值h(a);
(2)对(1)中的h(a),若关于a的方程h(a)=k(a+1)有两个不同的实数解,求实数k的取值范围;
(3)若点A(a1,h(a1)),B(a2,h(a2)),C(a3,h(a3)),从左到右依次是函数y=h(a)图象上三点,且这三点不共线,求证:△ABC是钝角三角形.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)f′(x)=6x2-4ax=6x(x-
a),令f′(x)=0,得x=0或x=
a.由此根据a的取值范围进行分类讨论,能求出函数f(x)在区间[1,2]上的最小值.
(2)令y=k(a+1),得y=h(a)图象与直线y=k(a+1)有两个不同的交点,由直线y=k(a+1)恒过定点(-1,0),能求出实数k的取值范围.
(3).设a1<a2<a3,由(2)知h(a1)>h(a2)>h(a3),由已知条件推导出
•
<0,由此能证明△ABC为钝角三角形.
| 2 |
| 3 |
| 2 |
| 3 |
(2)令y=k(a+1),得y=h(a)图象与直线y=k(a+1)有两个不同的交点,由直线y=k(a+1)恒过定点(-1,0),能求出实数k的取值范围.
(3).设a1<a2<a3,由(2)知h(a1)>h(a2)>h(a3),由已知条件推导出
| BA |
| BC |
解答:
(1)解:∵f(x)=2x2(x-a),
∴f′(x)=6x2-4ax=6x(x-
a),
令f′(x)=0,得x=0或x=
a.
①若a<
,即0<
a<1时,
则当1≤x≤2时,f′(x)>0,∴f(x)在区间[1,2]上是增函数,
∴h(a)=f(1)-2a.
②若
≤a<3,即1≤
a<2时,
则当
a<x≤2时,f′(x)>0,
∴f(x)在区间[1,
a]上是减函数,在[
a,2]上是增函数,
∴h(a)=f(
a)=-
a3
②若a≥3,即
a≥2时,当1≤x≤2时,f′(x)≤0,
∴f(x)在区间[1,2]上是减函数,
∴h(a)=f(2)=16-8a,
综上所述,函数f(x)在区间[1,2]上的最小值是:
h(a)=
…(8分)
(2)解:∵方程h(a)=k(a+1)有两个不同的实数解,
令y=k(a+1),得y=h(a)图象与直线y=k(a+1)有两个不同的交点,
而直线y=k(a+1)恒过定点(-1,0),
∴实数k的取值范围是(-8,-2).…(12分)
(3).证明:不妨设a1<a2<a3,
由(2)知h(a1)>h(a2)>h(a3),
=(a1-a2,h(a1)-h(a2)),
=(a3-a2,h(a3)-h(a2)),
∴
•
=(a1-a2)(a3-a2)+[h(a1)-h(a2)],
∵a1-a2<0,a3-a2>0,h(a1)-h(a2)>0,h(a3)-h(a2)<0,
∴
•
<0.又∵A,B,C三点不共线,
∴∠B∈(
,π),即△ABC为钝角三角形…(16分)
∴f′(x)=6x2-4ax=6x(x-
| 2 |
| 3 |
令f′(x)=0,得x=0或x=
| 2 |
| 3 |
①若a<
| 3 |
| 2 |
| 2 |
| 3 |
则当1≤x≤2时,f′(x)>0,∴f(x)在区间[1,2]上是增函数,
∴h(a)=f(1)-2a.
②若
| 3 |
| 2 |
| 2 |
| 3 |
则当
| 2 |
| 3 |
∴f(x)在区间[1,
| 2 |
| 3 |
| 2 |
| 3 |
∴h(a)=f(
| 2 |
| 3 |
| 3 |
| 27 |
②若a≥3,即
| 2 |
| 3 |
∴f(x)在区间[1,2]上是减函数,
∴h(a)=f(2)=16-8a,
综上所述,函数f(x)在区间[1,2]上的最小值是:
h(a)=
|
(2)解:∵方程h(a)=k(a+1)有两个不同的实数解,
令y=k(a+1),得y=h(a)图象与直线y=k(a+1)有两个不同的交点,
而直线y=k(a+1)恒过定点(-1,0),
∴实数k的取值范围是(-8,-2).…(12分)
(3).证明:不妨设a1<a2<a3,
由(2)知h(a1)>h(a2)>h(a3),
| BA |
| BC |
∴
| BA |
| BC |
∵a1-a2<0,a3-a2>0,h(a1)-h(a2)>0,h(a3)-h(a2)<0,
∴
| BA |
| BC |
∴∠B∈(
| π |
| 2 |
点评:本题考查函数在闭区间上最小值的求法,考查实数的取值范围的求法,考查三角形为钝角三角形的证明,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目
已知函数f(x)=
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
|
| A、(2,2014) |
| B、(2,2015) |
| C、(3,2014) |
| D、(3,2015) |
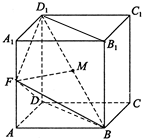 如图,已知在棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.
如图,已知在棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.