题目内容
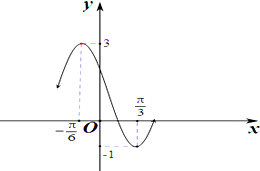已知函数g（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜| π |
| 2 |
（1）将函数g（x）的图象保持纵坐标不变，横坐标向右平移
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
（2）求使f（x）≥2的x的取值范围的集合．
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（1）由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，可得函数g（x）的解析式．
再根据函数y=Acos（ωx+φ）+B的图象的平移变换规律，可得f（x）的解析式，再根据x∈[-
，
]，利用余弦函数的定义域和值域求得可得f（x）的值域．
（2）由f（x）≥2可得 cos（2x-
）≥
，故有2kπ-
≤2x-
≤2kπ+
，k∈z，由此求得不等式的解集．
再根据函数y=Acos（ωx+φ）+B的图象的平移变换规律，可得f（x）的解析式，再根据x∈[-
| π |
| 6 |
| π |
| 3 |
（2）由f（x）≥2可得 cos（2x-
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：
解：（1）由题意可得B=
=1，A=3-1=2，
=
•
=
+
，解得ω=2．
再由五点法作图可得 2×（-
）+φ=0，求得φ=
，∴函数g（x）=2cos（2x+
）+1．
将函数g（x）的图象保持纵坐标不变，横坐标向右平移
个单位后得到函数f（x）的图象，
则函数f（x）=2cos[2（x-
）+
]+1=2cos（2x-
）+1．
由x∈[-
，
]，可得 2x-
∈[-
，
]，∴f（x）∈[0，3]．
（2）由f（x）≥2，可得 cos（2x-
）≥
，∴2kπ-
≤2x-
≤2kπ+
，k∈z，
求得 kπ≤x≤kπ+
，k∈z，故不等式的解集为[kπ，kπ+
]，k∈z．
| 3+(-1) |
| 2 |
| T |
| 2 |
| 1 |
| 2 |
| 2π |
| ω |
| π |
| 3 |
| π |
| 6 |
再由五点法作图可得 2×（-
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
将函数g（x）的图象保持纵坐标不变，横坐标向右平移
| π |
| 3 |
则函数f（x）=2cos[2（x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
由x∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
（2）由f（x）≥2，可得 cos（2x-
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
求得 kπ≤x≤kπ+
| π |
| 3 |
| π |
| 3 |
点评：本题主要考查由函数y=Acos（ωx+φ）+B的部分图象求解析式，函数y=Acos（ωx+φ）+B的图象的平移变换规律，余弦函数的定义域和值域，三角不等式的解法，属于基础题．
练习册系列答案
相关题目
函数y=sinx•cosx，x∈R的最小正周期是（ ）
| A、4π | ||
B、
| ||
| C、2π | ||
| D、π |