题目内容
全集U={a，b，c，d，e}，M={a，d}，N={a，c，e}，则N∩∁UM为（ ）
| A、{c，e} |
| B、{a，c} |
| C、{d，e} |
| D、{a，e} |
考点：交、并、补集的混合运算
专题：集合
分析：根据全集U及M求出M的补集，找出N与M补集的交集即可．
解答：
解：∵全集U={a，b，c，d，e}，M={a，d}，N={a，c，e}，
∴∁UM={b，c，e}，
则N∩∁UM={c，e}．
故选：A．
∴∁UM={b，c，e}，
则N∩∁UM={c，e}．
故选：A．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
点A（2a，a-1）在以点C（0，1）为圆心，
为半径的圆上，则a的值为（ ）
| 5 |
| A、±1 | ||
| B、0或1 | ||
C、-1或
| ||
D、1或-
|
若集合M={x|y=
}，N={x|y=
}，则M∩N=（ ）
| x2-x3 |
2-(
|
| A、[-1，1] |
| B、[0，1] |
| C、（-∞，0]∪（[1，+∞） |
| D、（-∞，-1]∪[1，+∞） |
方程ax2+by2=1表示双曲线的必要不充分条件是（ ）
| A、a＜0且b＞0 |
| B、a＞0且b＜0 |
| C、ab＜5 |
| D、ab＞0 |
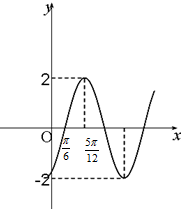函数f（x）=2sin（ωx+φ），（ω＞0，-| π |
| 2 |
| π |
| 2 |
A、向右平移
| ||||
B、向右平移
| ||||
C、向右平移
| ||||
D、向右平移
|
若复数z满足（-1+i）z=2，则下面四个命题中真命题的为（ ）
p1：|z|=2
p2：z2是纯虚数
p3：z的共轭复数为1+i
p4：z的虚部为-1．
p1：|z|=2
p2：z2是纯虚数
p3：z的共轭复数为1+i
p4：z的虚部为-1．
| A、p1，p2 |
| B、p2，p3 |
| C、p3，p4 |
| D、p2，p4 |