题目内容
若集合M={x|y=
}，N={x|y=
}，则M∩N=（ ）
| x2-x3 |
2-(
|
| A、[-1，1] |
| B、[0，1] |
| C、（-∞，0]∪（[1，+∞） |
| D、（-∞，-1]∪[1，+∞） |
考点：指、对数不等式的解法
专题：函数的性质及应用,集合
分析：解根式不等式求得M，解指数不等式求得N，再利用两个集合的交集的定义求得M∩N．
解答：
解：集合M={x|y=
}={x|x2-x3≥0}={x|x≤1}，
N={x|y=
}={x|2-(
)x≥0}={x|x≥-1}，
则M∩N=[-1，1]，
故选：A．
| x2-x3 |
N={x|y=
2-(
|
| 1 |
| 2 |
则M∩N=[-1，1]，
故选：A．
点评：本题主要考查指数不等式、根式不等式的解法，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
已知中心在坐标原点，焦点在坐标轴上的双曲线的渐近线方程为y=±
x则该双曲线的离心率为（ ）
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
C是以原点O为中心，焦点在y轴上的等轴双曲线在第一象限部分，曲线C在点P处的切线分别交该双曲线的两条渐近线于A，B两点，则（ ）
A、|OP|＜
| ||
| B、|OP|=|AB| | ||
C、
| ||
D、|OP|=
|
某几何体的三视图如图所示，则它的表面积是（ ）
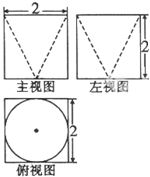
A、24+
| ||
| B、24-π | ||
C、24+(
| ||
D、20+(
|
已知中心在坐标原点，焦点在y轴上的双曲线的渐近线方程为y=±
x，则此双曲线的离心率为（ ）
| 1 |
| 2 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
全集U={a，b，c，d，e}，M={a，d}，N={a，c，e}，则N∩∁UM为（ ）
| A、{c，e} |
| B、{a，c} |
| C、{d，e} |
| D、{a，e} |
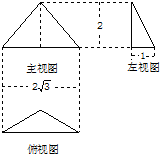已知一个三棱锥的三视图如图所示，其中俯视图是等腰三角形，则该三棱锥的体积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、2
|