题目内容
有如下四个命题:
①命题“若x2-3x+2=0,则x=1“的逆否命题为“若x≠1,则x2-3x+2≠0”.
②若x=y=0,则x2+y2=0的逆命题是真命题.
③若p∧q为假命题,则p,q均为假命题.
④命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”.
其中错误命题的个数是( )
①命题“若x2-3x+2=0,则x=1“的逆否命题为“若x≠1,则x2-3x+2≠0”.
②若x=y=0,则x2+y2=0的逆命题是真命题.
③若p∧q为假命题,则p,q均为假命题.
④命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”.
其中错误命题的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:阅读型,简易逻辑
分析:由原命题与逆否命题的关系即可判断①;写出原命题的逆命题,然后判断真假即可判断②;由复合命题p∧q的真值表可判断③;由原命题与否命题的关系即可判断④.
解答:
解:①“若p则q”的逆否命题为“若¬q则¬p”,故①正确;
②“若x=y=0,则x2+y2=0”的逆命题是“若x2+y2=0,则x=y=0”,比如令x=i,y=1,有i2+12=0,但x≠y,故②不正确;
③若p∧q为假命题,则p,q中至少有一个是假命题,故③不正确;
④命题“若x2=1,则x=1”的否命题是“若x2≠1,则x≠1”,故④不正确.
即错误命题的个数为3.
故选:D.
②“若x=y=0,则x2+y2=0”的逆命题是“若x2+y2=0,则x=y=0”,比如令x=i,y=1,有i2+12=0,但x≠y,故②不正确;
③若p∧q为假命题,则p,q中至少有一个是假命题,故③不正确;
④命题“若x2=1,则x=1”的否命题是“若x2≠1,则x≠1”,故④不正确.
即错误命题的个数为3.
故选:D.
点评:本题考查简易逻辑的基础知识:四种命题及其真假,复合命题的真假,注意p且q假,p,q中至少有一个假;p或q真,p,q中至少有一个真.解题时特别注意否命题与命题的否定的区别,本题属于基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
已知中心在坐标原点,焦点在坐标轴上的双曲线的渐近线方程为y=±
x则该双曲线的离心率为( )
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
全集U={a,b,c,d,e},M={a,d},N={a,c,e},则N∩∁UM为( )
| A、{c,e} |
| B、{a,c} |
| C、{d,e} |
| D、{a,e} |
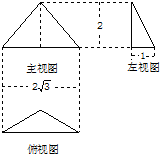 已知一个三棱锥的三视图如图所示,其中俯视图是等腰三角形,则该三棱锥的体积为( )
已知一个三棱锥的三视图如图所示,其中俯视图是等腰三角形,则该三棱锥的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知一个几何体的正视图是直径为2的圆,侧视图、俯视图都是边长为2的正方形,则该几何体的体积为( )
| A、2π | B、4π | C、6π | D、8π |
已知
=(1,-1),
=(λ,1),
与
的夹角为钝角,则λ的取值范围是( )
| a |
| b |
| a |
| b |
| A、λ>1 |
| B、λ<1 |
| C、λ<-1 |
| D、λ<-1或-1<λ<1 |
某几何体的三视图如图所示,则该几何体的体积为( )


| A、8π+16 | B、8π-16 |
| C、8π+8 | D、16π-8 |