题目内容
方程ax2+by2=1表示双曲线的必要不充分条件是( )
| A、a<0且b>0 |
| B、a>0且b<0 |
| C、ab<5 |
| D、ab>0 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:结合双曲线的定义和方程,利用充分条件和必要条件的定义进行判断.
解答:
解:若方程ax2+by2=1表示双曲线,
则方程等价为
+
=1,即
•
<0,
∴ab<0.
即a>0且b<0或a<0且b>0,
则A,B是充分不必要条件,
C是必要不充分条件,
D是既不充分也不必要条件.
故选:C.
则方程等价为
| x2 | ||
|
| y2 | ||
|
| 1 |
| a |
| 1 |
| b |
∴ab<0.
即a>0且b<0或a<0且b>0,
则A,B是充分不必要条件,
C是必要不充分条件,
D是既不充分也不必要条件.
故选:C.
点评:本题主要考查充分条件和必要条件的应用,利用双曲线的定义和方程求出ab<0是解决本题的关键,比较基础.

练习册系列答案
相关题目
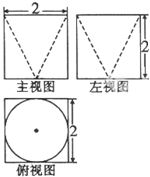
某几何体的三视图如图所示,则它的表面积是( )

A、24+
| ||
| B、24-π | ||
C、24+(
| ||
D、20+(
|
命题“?x∈R,2x2-x+1<0”的否定是( )
| A、?x∈R,2x2-x+1≥0 |
| B、?x∈R,2x2-x+1≥0 |
| C、?x∈R,2x2-x+1≤0 |
| D、?x∈R,2x2-x+1<0 |
全集U={a,b,c,d,e},M={a,d},N={a,c,e},则N∩∁UM为( )
| A、{c,e} |
| B、{a,c} |
| C、{d,e} |
| D、{a,e} |
已知双曲线的中心在原点,两个焦点F1,F2分别为(
,0)和(-
,0),点P在双曲线上且PF1⊥PF2,且△PF1F2的面积为1,则双曲线的方程为( )
| 5 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
已知一个几何体的正视图是直径为2的圆,侧视图、俯视图都是边长为2的正方形,则该几何体的体积为( )
| A、2π | B、4π | C、6π | D、8π |