题目内容
若复数z满足(-1+i)z=2,则下面四个命题中真命题的为( )
p1:|z|=2
p2:z2是纯虚数
p3:z的共轭复数为1+i
p4:z的虚部为-1.
p1:|z|=2
p2:z2是纯虚数
p3:z的共轭复数为1+i
p4:z的虚部为-1.
| A、p1,p2 |
| B、p2,p3 |
| C、p3,p4 |
| D、p2,p4 |
考点:复数的代数表示法及其几何意义,复数的基本概念
专题:数系的扩充和复数
分析:把给出的等式两边同时乘以
,利用复数代数形式的除法运算求出复数z,进一步求得|z|,z2,
及z的虚部,然后逐一核对四个命题得答案.
| 1 |
| -1+i |
. |
| z |
解答:
解:由(-1+i)z=2,得
z=
=
=
=-1-i,
∴|z|=
=
;
z2=(-1-i)2=(1+i)2=2i;
=-1+i;
z的虚部是-1.
∴命题p2,p4是真命题.
故选:D.
z=
| 2 |
| -1+i |
| 2(-1-i) |
| (-1+i)(-1-i) |
| -2-2i |
| 2 |
∴|z|=
| (-1)2+(-1)2 |
| 2 |
z2=(-1-i)2=(1+i)2=2i;
. |
| z |
z的虚部是-1.
∴命题p2,p4是真命题.
故选:D.
点评:本题考查复数代数形式的除法运算,考查复数的基本概念,是基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
某几何体的三视图如图所示,则它的表面积是( )
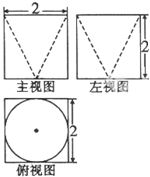

A、24+
| ||
| B、24-π | ||
C、24+(
| ||
D、20+(
|
全集U={a,b,c,d,e},M={a,d},N={a,c,e},则N∩∁UM为( )
| A、{c,e} |
| B、{a,c} |
| C、{d,e} |
| D、{a,e} |
已知双曲线的中心在原点,两个焦点F1,F2分别为(
,0)和(-
,0),点P在双曲线上且PF1⊥PF2,且△PF1F2的面积为1,则双曲线的方程为( )
| 5 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2-
|
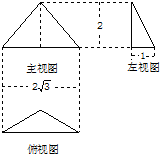 已知一个三棱锥的三视图如图所示,其中俯视图是等腰三角形,则该三棱锥的体积为( )
已知一个三棱锥的三视图如图所示,其中俯视图是等腰三角形,则该三棱锥的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知一个几何体的正视图是直径为2的圆,侧视图、俯视图都是边长为2的正方形,则该几何体的体积为( )
| A、2π | B、4π | C、6π | D、8π |
某几何体的三视图如图所示,则该几何体的体积为( )


| A、8π+16 | B、8π-16 |
| C、8π+8 | D、16π-8 |