题目内容
甲、乙、丙三个同学同时报名参加某重点高校2014年自主招生,高考前自主招生的程序为审核材料和文化测试,只有审核过关后才能参加文化测试,文化测试合格者即可获得自主招生入选资格.因为甲,乙,丙三人各有优势,甲,乙,丙三人审核材料过关的概率分别为
,
,
,审核过关后,甲,乙,丙三人文化测试合格的概率分别为
,
,
.
(Ⅰ)求甲,乙,丙三人中只有一人获得自主招生入选资格的概率;
(Ⅱ)设甲,乙,丙三人中材料审核过关的人数为随机变量X,求X的分布列和期望.
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 3 |
| 4 |
(Ⅰ)求甲,乙,丙三人中只有一人获得自主招生入选资格的概率;
(Ⅱ)设甲,乙,丙三人中材料审核过关的人数为随机变量X,求X的分布列和期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(I)设甲,乙,丙三人获得自主招生入选资格的概率分别为P(A)、P(B)、P(C),由题意得P(A)=
×
=
,P(B)=
×
=
,P(C)=
×
=
,由此能求出甲,乙,丙三人中只有一人获得自主招生入选资格的概率.
(Ⅱ)X可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和期望.
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 2 |
| 5 |
| 3 |
| 4 |
| 3 |
| 10 |
(Ⅱ)X可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和期望.
解答:
解:(I)设甲,乙,丙三人获得自主招生入选资格的概率分别为P(A)、P(B)、P(C),
则P(A)=
×
=
,P(B)=
×
=
,P(C)=
×
=
,
所以甲,乙,丙三人中只有一人获得自主招生入选资格的概率:
P=
(1-
)2=0.441
(Ⅱ)X可能取值为0,1,2,3,
则P(X=0)=(1-
)(1-
)(1-
)=
,
P(X=1)=
×
×
+
×
×
+
×
×
=
,
P(X=2)=
×
×
+
×
×
+
×
×
=
,
P(X=3)=
×
×
=
,
∴X的分布列为:
EX=0×
+1×
+2×
+3×
=
.
则P(A)=
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 2 |
| 5 |
| 3 |
| 4 |
| 3 |
| 10 |
所以甲,乙,丙三人中只有一人获得自主招生入选资格的概率:
P=
| C | 1 3 |
| 3 |
| 10 |
| 3 |
| 10 |
(Ⅱ)X可能取值为0,1,2,3,
则P(X=0)=(1-
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 25 |
P(X=1)=
| 1 |
| 2 |
| 2 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
| 2 |
| 5 |
| 19 |
| 50 |
P(X=2)=
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 1 |
| 2 |
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
| 19 |
| 50 |
P(X=3)=
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 25 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 3 |
| 25 |
| 19 |
| 50 |
| 19 |
| 50 |
| 6 |
| 50 |
| 3 |
| 2 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
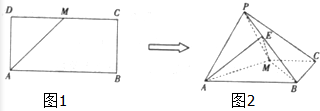 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
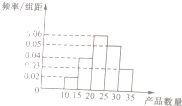 为了调查某厂数万名工人独立生产某种产品的能力,随机抽查了m位工人某天独立生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35),频率分布直方图如图所示,已知独立生产的产品数量在[20,25)之间的工人有6位.
为了调查某厂数万名工人独立生产某种产品的能力,随机抽查了m位工人某天独立生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35),频率分布直方图如图所示,已知独立生产的产品数量在[20,25)之间的工人有6位.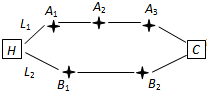 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为