题目内容
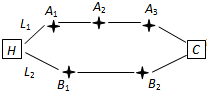 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 5 |
(1)若走路线L1,求最多遇到1次红灯的概率;
(2)王先生经过研究得到途中所产生的费用如表:
| 路线 | 距离(公里) | 行驶费用(元/公里) | 遇红灯时 费用(元/次) |
| L1 | 20 | 1.5 | 1.5 |
| L2 | 30 | 1 | 1 |
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(1)走路线L1最多遇到1次红灯含两种情况:没有遇到红灯和恰好遇到一次红灯,由此能求出走路线L1最多遇到1次红灯的概率.
(2)分别求出选择路线L1和选择路线L2的期望和方差,由此能做正正确判断.
(2)分别求出选择路线L1和选择路线L2的期望和方差,由此能做正正确判断.
解答:
解:(1)设“走路线L1最多遇到1次红灯”为事件A,
则P(A)=C
×(
)3+C
×
×(
)2=
.
所以走路线L1最多遇到1次红灯的概率为
.…(4分)
(2)若选择路线L1:
E(m)=32.25,D(m)=1.6875;
若选择路线L2:
E(m)=31.35,D(m)=0.4275.
答:综合考虑应选择路线L2上班更好.…(12分)
则P(A)=C
0 3 |
| 1 |
| 2 |
1 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以走路线L1最多遇到1次红灯的概率为
| 1 |
| 2 |
(2)若选择路线L1:
| 费用m | 30 | 31.5 | 33 | 34.5 |
| 概率P | 0.125 | 0.375 | 0.375 | 0.125 |
若选择路线L2:
| 费用n | 30 | 31 | 32 |
| 概率P | 0.1 | 0.45 | 0.45 |
答:综合考虑应选择路线L2上班更好.…(12分)
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法及应用,是中档题.

练习册系列答案
相关题目

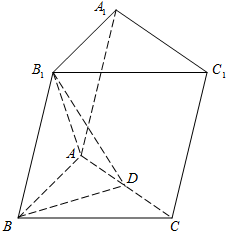 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.