题目内容
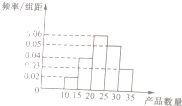 为了调查某厂数万名工人独立生产某种产品的能力,随机抽查了m位工人某天独立生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35),频率分布直方图如图所示,已知独立生产的产品数量在[20,25)之间的工人有6位.
为了调查某厂数万名工人独立生产某种产品的能力,随机抽查了m位工人某天独立生产该产品的数量,产品数量的分组区间为[10,15),[15,20),[20,25),[25,30),[30,35),频率分布直方图如图所示,已知独立生产的产品数量在[20,25)之间的工人有6位.(Ⅰ)求m的值;
(Ⅱ)工厂规定:若独立生产产品数量当日不小于25,则该工人当选“生产之星”,若将这天独立生产该产品数量的频率视为概率,随机从全厂工人中抽取3人,这3人中当日“生产之星”人数为X,求X的分布列及数学期望E(X).
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由频率分布直方图可得产品数量在[20,25)之间的频率为0.3,继而求出m的值,
(Ⅱ)X的取值为0,1,2,3,由题知X~B(3,
),求出相应的概率,列出分布列,求出数学期望.
(Ⅱ)X的取值为0,1,2,3,由题知X~B(3,
| 2 |
| 5 |
解答:
解:(Ⅰ)由频率分布直方图可得产品数量在[20,25)之间的频率为0.3,
所以
=0.3即m=20
(Ⅱ)由频率分布直方图可得产品数量不小于25的频率为0.4,
所以三人中每人是“生产之星”的概率都是
,
X的取值为0,1,2,3,由题知X~B(3,
),
P(X=0)=(
)3=
,P(X=1)=
×
×(
)2=
,
P(X=2)=
×(
)2×
=
,P(X=3)=(
)3=
所以X的分布列为
所以E(X)=0×
+1×
+2×
+3×
=
.
所以
| 6 |
| m |
(Ⅱ)由频率分布直方图可得产品数量不小于25的频率为0.4,
所以三人中每人是“生产之星”的概率都是
| 2 |
| 5 |
X的取值为0,1,2,3,由题知X~B(3,
| 2 |
| 5 |
P(X=0)=(
| 3 |
| 5 |
| 27 |
| 125 |
| C | 1 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 54 |
| 125 |
P(X=2)=
| C | 2 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 36 |
| 125 |
| 2 |
| 5 |
| 8 |
| 125 |
所以X的分布列为
| X | 0 | 1 | 2 | 3 | ||||||||
P |
|
|
|
|
| 27 |
| 125 |
| 54 |
| 125 |
| 36 |
| 125 |
| 8 |
| 125 |
| 6 |
| 5 |
点评:本题考查频率分布直方图以及二项分布,离散型随机变量的分布列数学期望、考查运用概率知识解决实际问题的能力.

练习册系列答案
相关题目
 如图矩形ORTM内放置5个大小相同的正方形,其中A,B,C,D都在矩形的边上,若向量
如图矩形ORTM内放置5个大小相同的正方形,其中A,B,C,D都在矩形的边上,若向量