题目内容
15.已知等差数列{an}的首项为1,公差为3,若Sn=35,则n=5.分析 由等差数列{an}的首项为1,公差为3,求出Sn=$\frac{3}{2}{n}^{2}-\frac{1}{2}n$,再由Sn=35,得${S}_{n}=\frac{3}{2}{n}^{2}-\frac{1}{2}n=35$,由此能求出结果.
解答 解:∵等差数列{an}的首项为1,公差为3,
∴${S}_{n}=n{a}_{1}+\frac{n(n-1)}{2}d$=n+$\frac{n(n-1)}{2}×3$=$\frac{3}{2}{n}^{2}-\frac{1}{2}n$,
∵Sn=35,∴${S}_{n}=\frac{3}{2}{n}^{2}-\frac{1}{2}n=35$,
解得n=5或n=-$\frac{14}{3}$(舍).
故答案为:5.
点评 本题考查等差数列的前n项和为35的项数n的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
6.函数y=sinx的一个递减区间是( )
| A. | (0,π) | B. | $[{\frac{π}{2},\frac{3π}{2}}]$ | C. | $[{-\frac{π}{2},\frac{π}{2}}]$ | D. | (π,2π) |
6.圆的参数方程为:$\left\{\begin{array}{l}{x=2+2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数).则圆的圆心坐标为( )
| A. | (0,2) | B. | (0,-2) | C. | (-2,0) | D. | (2,0) |
3.已知两个等差数列{an}和{bn}的前n项和分别为An和Bn,且$\frac{A_n}{B_n}=\frac{7n+57}{n+3}$,则使得$\frac{a_n}{b_n}$为整数的正整数n的个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
10.若$sinα=\frac{1}{3}$,则cos2α的值等于( )
| A. | $\frac{7}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{{4\sqrt{2}}}{9}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
20.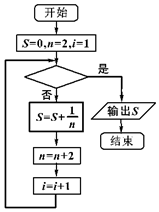 如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )
如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )
 如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )
如图,给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+…+\frac{1}{22}$的一个程序框图,其中判断框内应填入的条件是( )| A. | i<11 | B. | i>11 | C. | i<22 | D. | i>22 |
3.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如下表:
(1)画出茎叶图;
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)数据的平均数、方差,并判断选谁参加比赛更合适?
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)数据的平均数、方差,并判断选谁参加比赛更合适?
3.等差数列{an}的前11项和S11=88,则a3+a6+a9=( )
| A. | 18 | B. | 24 | C. | 30 | D. | 32 |