题目内容
3．等差数列{an}的前11项和S11=88，则a3+a6+a9=（ ）| A． | 18 | B． | 24 | C． | 30 | D． | 32 |
分析 由等差数列{an}的前11项和S11=88，求出a6=8，由此利用a3+a6+a9=3a6，能求出结果．
解答 解：∵等差数列{an}的前11项和S11=88，
∴${S}_{11}=\frac{11}{2}（{a}_{1}+{a}_{11}）=11{a}_{6}$=88，
解得a6=8，
∴a3+a6+a9=3a6=24．
故选：B．
点评 本题考查等差数列的三项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
11．
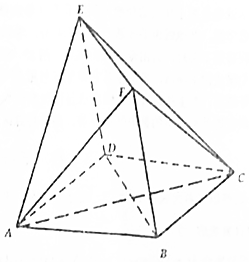如图，四边形ABCD与BDEF均为菱形，∠DAB=∠DBF=60°，且FA=FC；
（1）求证：AC⊥平面BDEF；
（2）求证：FC∥平面EAD；
（3）设AB=BF=a，求四面体A-BCF的体积．
如图，四边形ABCD与BDEF均为菱形，∠DAB=∠DBF=60°，且FA=FC；（1）求证：AC⊥平面BDEF；
（2）求证：FC∥平面EAD；
（3）设AB=BF=a，求四面体A-BCF的体积．
11．已知tanα=3，则2sin2α-sinαcosα+cos2α的值等于（ ）
| A． | $\frac{8}{9}$ | B． | $\frac{7}{5}$ | C． | $\frac{2}{5}$ | D． | $\frac{8}{5}$ |