Question

16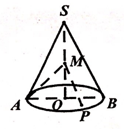．如图，圆锥的轴截面SAB是正三角形，O为底面中心，M为线段SO中点，动点P在圆锥底面内（包括圆周），若AM⊥MP，则点P的轨迹为（　　）

• A． 线段
• B． 圆
• C． 椭圆
• D． 抛物线

Answer 1

分析 设圆锥的轴截面SAB是边长为2的等边三角形，建立空间直角坐标系，写出点的坐标，设出动点的坐标，利用向量的坐标公式求出向量坐标，利用向量垂直的充要条件列出方程求出动点P的轨迹方程，得到P的轨迹是底面圆的弦．

解答 解：设圆锥的轴截面SAB是边长为2的等边三角形，建立空间直角坐标系．设A（0，-1，0），B（0，1，0），S（0，0，$\sqrt{3}$），M（0，0，$\frac{\sqrt{3}}{2}$），P（x，y，0）．
于是有$\overrightarrow{AM}$=（0，1，$\frac{\sqrt{3}}{2}$），$\overrightarrow{MP}$=（x，y，-$\frac{\sqrt{3}}{2}$）．
由于AM⊥MP，所以（0，1，$\frac{\sqrt{3}}{2}$）•（x，y，-$\frac{\sqrt{3}}{2}$）=0，
即y=$\frac{3}{4}$，此为P点形成的轨迹是底面圆的弦．
故选：A．

点评 本题考查通过建立坐标系，将求轨迹问题转化为求轨迹方程、考查向量的数量积公式、向量垂直的充要条件、圆的弦长的求法．属中档题．