题目内容
7.在直角坐标系xOy中,已知点P(1,-2),直线$l:\;\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=2+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$( t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,直线l和曲线C的交点为A、B.(1)求直线l和曲线C的普通方程;
(2)求|PA|+|PB|的值.
分析 (1)利用三种坐标的互化方法,求直线l和曲线C的普通方程;
(2)将直线l的标准参数方程代入曲线C:y2=2x中,得t2-6$\sqrt{2}$t+4=0,利用参数的几何意义求|PA|+|PB|的值.
解答 解:(1)直线$l:\;\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=2+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$( t为参数),消去t,可得直线l的普通方程为x-y-3=0;
曲线C的极坐标方程为ρsin2θ=2cosθ,即为ρ2sin2θ=2ρcosθ,
由x=ρcosθ,y=ρsinθ,可得曲线C的普通方程为 y2=2x;
(2)将直线l的标准参数方程代入曲线C:y2=2x中,
可得t2-6$\sqrt{2}$t+4=0,即有t1+t2=6$\sqrt{2}$,t1t2=4,由于t1>0,t2>0
则|PA|+|PB|=|t1|+|t2|=t1+t2=$6\sqrt{2}$.
点评 本题考查三种方程的互化,考查参数几何意义的运用,属于中档题.

练习册系列答案
相关题目
2.集合A={x||x-1|<2},B={x|$\frac{1}{9}$<3x<9},则A∩B=( )
| A. | (-1,3) | B. | (-1,2) | C. | (-2,2) | D. | (-2,3) |
19.如图是某几何体的三视图且a=b,则该几何体主视图的面积为( )
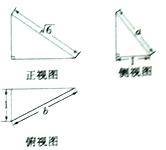

| A. | $\sqrt{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{15}}}{2}$ |
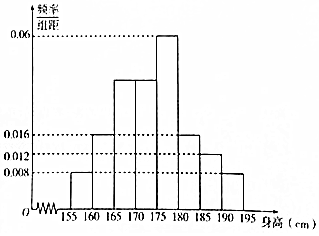 从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.
从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.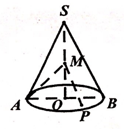 如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )
如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )