题目内容
4.已知圆C:x2+y2=4,直线l:ax+y+2a=0,当直线l与圆C相交于A,B两点,且|AB|=2$\sqrt{2}$时,求直线l的方程.分析 求出圆心到直线的距离,利用点到直线的距离公式,即可得出结论.
解答 解:圆C:x2+y2=4,圆心为(0,0),半径为2,
∵|AB|=2$\sqrt{2}$,
∴圆心到直线的距离为$\sqrt{4-2}$=$\sqrt{2}$,
∴$\frac{|2a|}{\sqrt{{a}^{2}+1}}$=$\sqrt{2}$
解得a=1或a=-1.…(8分)
故所求直线方程为x+y+2=0或x-y+2=0.…(10分)
点评 本题考查直线和圆的方程的应用,考查点到直线的距离公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.如图是某几何体的三视图且a=b,则该几何体主视图的面积为( )
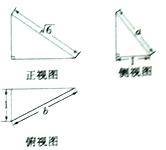

| A. | $\sqrt{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{15}}}{2}$ |
9.设a,b,c是三条不同的直线,α,β,γ是三个不同的平面,则下列命题正确的是( )
| A. | 若α⊥β,α⊥γ,则β⊥γ | B. | 若a,b与c所成的角相等,则a∥b | ||
| C. | 若α⊥α,α∥β,则α⊥β | D. | 若a∥b,a?α,则b∥α |
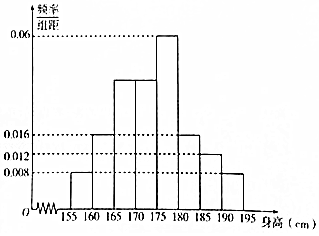 从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.
从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.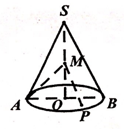 如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )
如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )