题目内容
5.已知f(x)=(logmx)2+2logmx-3(m>0,且m≠1).(Ⅰ)当m=2时,解不等式f(x)<0;
(Ⅱ)f(x)<0在[2,4]恒成立,求实数m的取值范围.
分析 (Ⅰ)当m=2时,可得(log2x)2+2log2x-3<0,即为-3<log2x<1,由对数函数的单调性,可得不等式的解集;
(Ⅱ)由f(x)<0在[2,4]恒成立,得-3<logmx<1在[2,4]恒成立,讨论m>1,0<m<1,解出x的范围,再由恒成立思想,可得m的范围.
解答 解:(Ⅰ)当m=2时,f(x)<0,
可得(log2x)2+2log2x-3<0,
即为-3<log2x<1,
解得$\frac{1}{8}$<x<2,
故原不等式的解集为{x|$\frac{1}{8}$<x<2};
(Ⅱ)由f(x)<0在[2,4]恒成立,
得-3<logmx<1在[2,4]恒成立,
①当m>1时,解得m-3<x<m,
即有m-3<2且4<m,
解得m>4;
②当0<m<1时,解得m<x<m-3,
即有m-3>4且m<2,
解得0<m<$\frac{1}{\root{3}{4}}$.
故实数m的取值范围是(0,$\frac{1}{\root{3}{4}}$)∪(4,+∞).
点评 本题考查对数不等式的解法,注意运用对数函数的单调性,考查不等式恒成立问题的解法,注意运用分类讨论思想方法,以及不等式的解法,考查化简整理的运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.设函数f(x)在(-∞,+∞)上有意义,对于给定的正数k,定义函数fk(x)=$\left\{\begin{array}{l}{f(x),f(x)<k}\\{k,f(x)≥k}\end{array}\right.$取k=3,f(x)=($\frac{k}{2}$)|x|,则fk(x)=$\frac{k}{2}$的零点有( )
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
4.已知曲线C1:y2=tx(y>0,t>0)在点M($\frac{4}{t}$,2)处的切线与曲线C2:y=ex+1-1也相切,则tln$\frac{4{e}^{2}}{t}$的值为( )
| A. | 4e2 | B. | 8e | C. | 2 | D. | 8 |
2.下列命题中正确的是( )
| A. | 若p∨q为真命题,则p∧q为真命题. | |
| B. | “x=5”是“x2-4x-5=0”的必要不充分条件. | |
| C. | 命题“?x∈R,x2+x-1<0”的否定为:“?x∈R,x2+x-1≥0”. | |
| D. | 命题“已知A,B为一个三角形两内角,若A=B,则sinA=sinB”的否命题为真命题. |
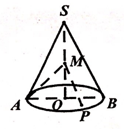 如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )
如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )