题目内容
6.某工厂生产甲、乙两种产品,每种产品都分为正品与次品.其中生产甲产品为正品的概率是$\frac{4}{5}$,生产乙产品为正品的概率是$\frac{3}{4}$;生产甲乙两种产品相互独立,互不影响.生产一件甲产品,若是正品可盈利40元,若是次品则亏损5元;生产一件乙产品,若是正品可盈利50元,若是次品则亏损10元.计算以下问题:(Ⅰ)记X为生产1件甲产品和1件乙产品所得的总利润,求随机变量X的分布列和数学期望;
(Ⅱ)求生产4件产品甲所获得的利润不少于110元的概率.
分析 (Ⅰ)根据随机变量X的所有取值,计算对应的概率,写出X的分布列,计算数学期望EX;
(Ⅱ)计算“生产4件芯片甲所获得的利润不少于110元”的概率值即可.
解答 解:(Ⅰ)随机变量X的所有取值为90,45,30,-15;
P(X=90)=$\frac{4}{5}$×$\frac{3}{4}$=$\frac{3}{5}$;P(X=45)=$\frac{1}{5}$×$\frac{3}{4}$=$\frac{3}{20}$;
P(X=30)=$\frac{4}{5}$×$\frac{1}{4}$=$\frac{1}{5}$;P(X=-15)=$\frac{1}{5}$×$\frac{1}{4}$=$\frac{1}{20}$.
所以,随机变量X的分布列为:
| X | 90 | 45 | 30 | -15 |
| P | $\frac{3}{5}$ | $\frac{3}{20}$ | $\frac{1}{5}$ | $\frac{1}{20}$ |
(Ⅱ)设“生产4件芯片甲所获得的利润不少于110元”为事件A,
则$P(A)={(\frac{4}{5})^4}+C_4^3{(\frac{4}{5})^3}\frac{1}{5}=\frac{512}{625}$.…(12分)
点评 本题考查了离散型随机变量的分布列与数学期望,以及概率的计算问题,是基础题目.

练习册系列答案
相关题目
1.设F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使得$(\overrightarrow{OP}+\overrightarrow{O{F_2}})•\overrightarrow{{F_2}P}=0$,其中O为坐标原点,且$|\overrightarrow{P{F_1}}|=3|\overrightarrow{P{F_2}}|$,则该双曲线的离心率为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | $\frac{5}{2}$ |
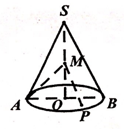 如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )
如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )