题目内容
1．若复数z=（1+ai）（1-i）为纯虚数，i是虚数单位，则实数a的值是-1，|$\overline{z}+i$|=3．分析 直接由复数代数形式的乘法运算化简复数z，再由已知条件列出方程组，求解得a的值，再求出$\overline{z}$，由复数求模公式计算得答案．
解答 解：∵z=（1+ai）（1-i）=a+1+（a-1）i为纯虚数，
∴$\left\{\begin{array}{l}{a+1=0}\\{a-1≠0}\end{array}\right.$，
解得a=-1．
∴z=-2i，则$\overline{z}=2i$．
∴|$\overline{z}+i$|═|2i+i|=|3i|=3．
故答案为：-1，3．
点评 本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
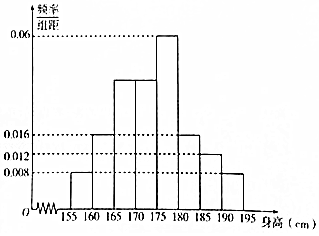从某校高一年级1000名学生中随机抽取100名测量身高，测量后发现被抽取的学生身高全部介于155厘米到195厘米之间，将测量结果分为八组：第一组[155，160），第二组[160，165），…，第八组[190，195），得到频率分布直方图如图所示．
9．设a，b，c是三条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是（ ）
| A． | 若α⊥β，α⊥γ，则β⊥γ | B． | 若a，b与c所成的角相等，则a∥b | ||
| C． | 若α⊥α，α∥β，则α⊥β | D． | 若a∥b，a?α，则b∥α |
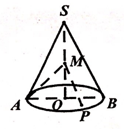如图，圆锥的轴截面SAB是正三角形，O为底面中心，M为线段SO中点，动点P在圆锥底面内（包括圆周），若AM⊥MP，则点P的轨迹为（ ）
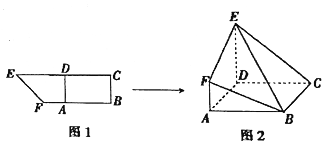如图所示，在直角梯形BCEF中，∠CBF=∠BCE=90°，A，D分别是BF，CE上的点，AD∥BC，且AB=DE=2BC=2AF（如图1），将四边形ADEF沿AD折起，连结BE、BF、CE（如图2）．在折起的过程中，下列结论错误的是④．（填序号）