题目内容
13.已知函数f(x)=$\left\{{\begin{array}{l}{{2^x},x≤0}\\{sinx,x>0}\end{array}}$,则$f(f(\frac{7π}{6}))$=( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
分析 先求出f($\frac{7π}{6}$)=sin$\frac{7π}{6}$=-sin$\frac{π}{6}$=-$\frac{1}{2}$,从而$f(f(\frac{7π}{6}))$=f(-$\frac{1}{2}$),由此能求出结果.
解答 解:∵函数f(x)=$\left\{{\begin{array}{l}{{2^x},x≤0}\\{sinx,x>0}\end{array}}$,
∴f($\frac{7π}{6}$)=sin$\frac{7π}{6}$=-sin$\frac{π}{6}$=-$\frac{1}{2}$,
$f(f(\frac{7π}{6}))$=f(-$\frac{1}{2}$)=${2}^{-\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
4.已知曲线C1:y2=tx(y>0,t>0)在点M($\frac{4}{t}$,2)处的切线与曲线C2:y=ex+1-1也相切,则tln$\frac{4{e}^{2}}{t}$的值为( )
| A. | 4e2 | B. | 8e | C. | 2 | D. | 8 |
5.设U=R,M={y|y=2x+1,-$\frac{1}{2}$≤x≤$\frac{1}{2}$},N={x|y=lg(x2+3x)},则(∁UM)∩N=( )
| A. | (-∞,-3]∪(2,+∞) | B. | (-∞,-3)∪(0,+∞) | C. | (-∞,-3)∪(2,+∞) | D. | (-∞,0)∪(2,+∞) |
2.下列命题中正确的是( )
| A. | 若p∨q为真命题,则p∧q为真命题. | |
| B. | “x=5”是“x2-4x-5=0”的必要不充分条件. | |
| C. | 命题“?x∈R,x2+x-1<0”的否定为:“?x∈R,x2+x-1≥0”. | |
| D. | 命题“已知A,B为一个三角形两内角,若A=B,则sinA=sinB”的否命题为真命题. |
3.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2为椭圆的左.右焦点,M是椭圆上任一点,若$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$的取值范围为[-3,3],则椭圆方程为( )
| A. | $\frac{x^2}{9}+\frac{y^2}{3}=1$ | B. | $\frac{x^2}{6}+\frac{y^2}{3}=1$ | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$+y2=1 |
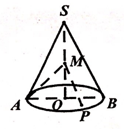 如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )
如图,圆锥的轴截面SAB是正三角形,O为底面中心,M为线段SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P的轨迹为( )