题目内容
20.设x,y是正数,且x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则$\frac{{b}_{1}{b}_{2}}{({a}_{1}+{a}_{2})^{2}}$的最大值是$\frac{1}{4}$.分析 x,y是正数,且x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,可得a1+a2=x+y,b1•b2=xy.可得$\frac{{b}_{1}{b}_{2}}{({a}_{1}+{a}_{2})^{2}}$=$\frac{xy}{(x+y)^{2}}$,再利用基本不等式的性质即可得出.
解答 解:∵x,y是正数,且x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,
∴a1+a2=x+y,b1•b2=xy.
则$\frac{{b}_{1}{b}_{2}}{({a}_{1}+{a}_{2})^{2}}$=$\frac{xy}{(x+y)^{2}}$$≤\frac{xy}{4xy}$=$\frac{1}{4}$,当且仅当x=y时取等号.
则$\frac{{b}_{1}{b}_{2}}{({a}_{1}+{a}_{2})^{2}}$的最大值是$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了等差数列与等比数列的通项公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知圆C:(x-6)2+(y-8)2=1和两点A(-m,0),B(m,0)(m>0),若对圆上任意一点P,都有∠APB<90°,则m的取值范围是( )
| A. | (9,10) | B. | (1,9) | C. | (0,9) | D. | (9,11) |
5.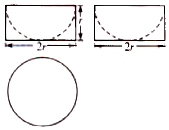 一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
 一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )| A. | 27π | B. | 36π | C. | 45π | D. | 54π |
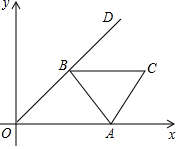 如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.
如图,边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动,∠AOD=30°,顶点B在射线,OD上随之移动,则线段CO的最大值为3$\sqrt{3}$+3.