题目内容
12．已知一个几何体的三视图及尺寸如图所示，则该几何体的内切球的半径是1．
分析 先判断三视图复原的几何体的形状，结合三视图的数据，确定斜高，高，再求几何体的内切球的半径．
解答 
解：三视图复原的几何体是正四棱锥，斜高是5cm，底面边长是8cm，高为3，
设内切球的半径为r，则利用三角函数可得$\frac{r}{3-r}$=$\frac{1}{2}$，
∴r=1．
故答案为：1．
点评 本题考查由三视图求几何体的内切球的半径，考查空间想象能力，属于基础题．
练习册系列答案
相关题目
7．某几何体的三视图如图所示，则该几何体的体积为（ ）
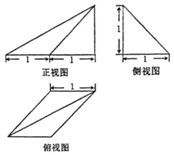
| A． | $\frac{1}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{3}$ |
4．已知某几何体的三视图如图所示，则该几何体的表面积为（ ）
| A． | $\frac{27}{2}$ | B． | 27 | C． | $27\sqrt{2}$ | D． | $27\sqrt{3}$ |
1．某三棱柱的三视图如图所示，该三棱柱的外接球的表面积为（ ）
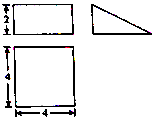
| A． | 32+8$\sqrt{5}$ | B． | 36π | C． | 18π | D． | $\frac{40\sqrt{10}}{3}$π |