题目内容
4.函数y=b+asinx(a<0)的最大值为-1,最小值为-5,(1)求a,b的值;
(2)求y=tan(3a+b)x的最小正周期.
分析 (1)利用三角函数的最值,求得a、b的值.
(2)利用正切函数的周期性,求得y=tan(3a+b)x的最小正周期.
解答 解:(1)∵函数y=b+asinx(a<0)的最大值为-1,最小值为-5,
∴$\left\{{\begin{array}{l}{b-a=-1}\\{b+a=-5}\end{array}}\right.∴\left\{{\begin{array}{l}{a=-2}\\{b=-3}\end{array}}\right.$,
(2)由(1)知y=tan(3a+b)x=tan(-6x-3x)=-tan9x,
故它的周期为$\frac{π}{9}$.
点评 本题主要考查三角函数的最值,正切函数的周期性,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
12. 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )
 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4}{3}$ | B. | 8 | C. | 4 | D. | $\frac{8}{3}$ |
1.某三棱柱的三视图如图所示,该三棱柱的外接球的表面积为( )
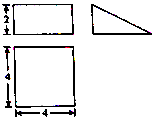

| A. | 32+8$\sqrt{5}$ | B. | 36π | C. | 18π | D. | $\frac{40\sqrt{10}}{3}$π |