题目内容
9.已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点F1(-$\sqrt{5}$,0),若椭圆上存在一点D,满足以椭圆短轴为直径的圆与线段DF1相切于线段DF1的中点F(1)求椭圆E的方程;
(2)过坐标原点O的直线交椭圆W:$\frac{{9{x^2}}}{{2{a^2}}}+\frac{{4{y^2}}}{b^2}$=1于P、A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连结AC并延长交椭圆W于B,求证:PA⊥PB.
分析 (I)用a,b,c表示出△OF1F的边长,利用勾股定理列方程解出a,b,即可;
(II)设P(m,n),用m,n表示出直线AC的方程,求出B点坐标,计算PA,PB的斜率即可得出结论.
解答 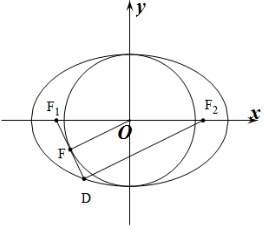 解:(Ⅰ)连接DF2,FO(O为原点,F2为右焦点),由题意知:椭圆的右焦点为${F_2}(\sqrt{5},0)$,
解:(Ⅰ)连接DF2,FO(O为原点,F2为右焦点),由题意知:椭圆的右焦点为${F_2}(\sqrt{5},0)$,
因为FO是△DF1F2的中位线,且DF1⊥FO,所以|DF2|=2|FO|=2b,
所以|DF1|=2a-|DF2|=2a-2b,故$|{F{F_1}}|=\frac{1}{2}|{D{F_1}}|=a-b$,
在Rt△FOF1中,${|{FO}|^2}+{|{F{F_1}}|^2}={|{{F_1}O}|^2}$,
即b2+(a-b)2=c2=5,又b2+5=a2,解得a2=9,b2=4,
所以椭圆E的方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$.
(Ⅱ)由(Ⅰ)得椭圆W的方程为$\frac{x^2}{2}+{y^2}=1$,
设P(m,n),则A(-m,-n),C(m,0),
∴${k_{PA}}=\frac{n}{m}$,${k_{AC}}=\frac{n}{2m}$,直线$AC:y=\frac{n}{2m}(x-m)$,
联立方程组$\left\{\begin{array}{l}y=\frac{n}{2m}(x-m)\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$,化简得$(1+\frac{n^2}{{2{m^2}}}){x^2}-\frac{n^2}{m}x+\frac{n^2}{2}-2=0$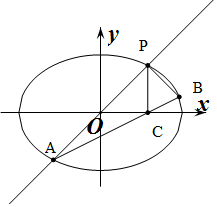 ,
,
∴${x_A}+{x_B}=\frac{{2m{n^2}}}{{2{m^2}+{n^2}}}$
因为xA=-m,所以${x_B}=\frac{{2{m^3}+3m{n^2}}}{{2{m^2}+{n^2}}}$,则${y_B}=\frac{n}{2m}{x_B}-\frac{n}{2}=\frac{n^3}{{2{m^2}+{n^2}}}$
所以${k_{PB}}=\frac{{\frac{n^3}{{2{m^2}+{n^2}}}-n}}{{\frac{{2{m^3}+3m{n^2}}}{{2{m^2}+{n^2}}}-m}}=-\frac{m}{n}$,
则kPA•kPB=-1,即PA⊥PB.
点评 本题考查了椭圆的定义,直线与椭圆的位置关系,属于中档题.

 阅读快车系列答案
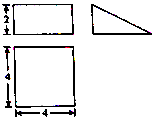
阅读快车系列答案 已知一个几何体的三视图如图所示,则该几何体的体积为( )
已知一个几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{4}{3}$ | B. | 8 | C. | 4 | D. | $\frac{8}{3}$ |

| A. | $\frac{27}{2}$ | B. | 27 | C. | $27\sqrt{2}$ | D. | $27\sqrt{3}$ |
| A. | $\frac{16}{3}π$ | B. | 16π | C. | $\frac{32}{3}π$ | D. | 32π |
| A. | 32+8$\sqrt{5}$ | B. | 36π | C. | 18π | D. | $\frac{40\sqrt{10}}{3}$π |
| A. | -5 | B. | 5 | C. | -4 | D. | 4 |