Question

8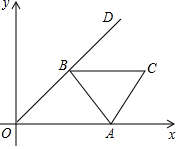．如图，边长为3的等边三角形ABC的顶点A在x轴的正半轴上移动，∠AOD=30°，顶点B在射线，OD上随之移动，则线段CO的最大值为3$\sqrt{3}$+3．

Answer 1

分析 连接OC，当OC垂直平分AB时，线段OC的长最大，根据正弦定理和两角差的正弦公式即可求出

解答 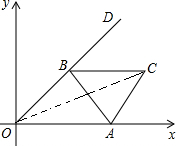解：如图：连接OC，当OC垂直平分AB时，OC最大．
此时∠ACO=30°，∠AOC=15°．
∴∠OCA=180°-30°-15°=135°，
在OCE中，由正弦定理可得$\frac{OC}{sin135°}$=$\frac{AC}{sin15°}$
∵sin15°=sin（45°-30°）=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$$\frac{\sqrt{6}-\sqrt{2}}{4}$
∴OC=3$\sqrt{3}$+3，
故答案为：3$\sqrt{3}$+3

点评 本题考查正弦定理和两角差的正弦公式，考查了学生的运算能力，属于基础题