题目内容
15.在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520个女性中6人患色盲.(Ⅰ)根据题中数据建立一个2×2的列联表;
(Ⅱ)在犯错误的概率不超过0.001的前提下,能否认为“性别与患色盲有关系”?
附:参考公式${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.
分析 (Ⅰ)根据题中数据,通过2×2的列联表方法,建立即可;
(Ⅱ)求出K2,然后判断即可.
解答 解:(Ⅰ)
| 患色盲 | 不患色盲 | 总计 | |
| 男 | 38 | 442 | 480 |
| 女 | 6 | 514 | 520 |
| 总计 | 44 | 956 | 1000 |
先算出k的观测值:$k=\frac{{1000×{{(38×514-442×6)}^2}}}{480×520×44×956}=27.14>10.828$,
则有P(K2≥10.828)=0.001,即H成立的概率不超过0.001,
故在犯错的概率不超过0.001的前提下,可以认为“性别与患色盲有关系”.
点评 本题考查独立检验思想方法应用,联列表的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
10.记f(n)为最接近$\sqrt{n}$(n∈N*)的整数,如f(1)=1,f(2)=1,f(3)=2,f(4)=2,f(5)=2,…,若$\frac{1}{f(1)}$+$\frac{1}{f(2)}$+$\frac{1}{f(3)}$+…+$\frac{1}{f(m)}$=4054,则正整数m的值为( )
| A. | 2016×2017 | B. | 20172 | C. | 2017×2018 | D. | 2018×2019 |
7.某几何体的三视图如图所示,则该几何体的体积为( )
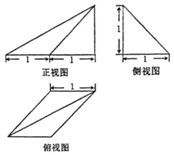

| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
4.已知某几何体的三视图如图所示,则该几何体的表面积为( )


| A. | $\frac{27}{2}$ | B. | 27 | C. | $27\sqrt{2}$ | D. | $27\sqrt{3}$ |