题目内容
5.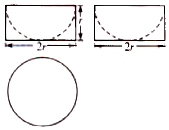 一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )
一个几何体的三视图如图所示,其中俯视图是半径为r的圆,若该几何体的体积为9π,则它的表面积是( )| A. | 27π | B. | 36π | C. | 45π | D. | 54π |
分析 几何体为圆柱中挖去一个半球,根据体积得出r,再计算表面积即可.
解答  解:几何体为圆柱中挖去一个半球,圆柱底面半径和高均为r,半球的半径为r,
解:几何体为圆柱中挖去一个半球,圆柱底面半径和高均为r,半球的半径为r,
∴几何体的体积V=π×r2•r-$\frac{1}{2}×\frac{4}{3}π{r}^{3}$=$\frac{1}{3}π{r}^{3}$=9π,∴r=3.
∴S侧=π×2r×r=2πr2=18π,S底=π×r2=9π,S半球=$\frac{1}{2}×4π×{r}^{2}$=2πr2=18π,
∴几何体的表面积为S表面积=18π+9π+18π=45π.
故选:C.
点评 本题考查了常见几何体及其组合体的三视图,面积与体积计算,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.条件p:|x+1|>2;条件q:{x|2<x<3},则?p是?q的( )
| A. | 必要不充分条件 | B. | 充要条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
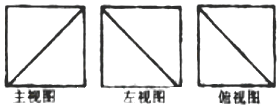
10.棱长为1的正方体截去一部分之后余下的几何体,其三视图如图所示,则余下几何体体积的最小值为( )

| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
14.已知△ABC的顶点都在半径为R的球O的球面上,球心O到平面ABC的距离为$\frac{{\sqrt{3}}}{2}R$,$AB=BC=AC=\sqrt{3}$,则球O的体积是( )
| A. | $\frac{16}{3}π$ | B. | 16π | C. | $\frac{32}{3}π$ | D. | 32π |