题目内容
已知向量
=（sinθ，1），
=（1，cosθ），其中0＜θ＜π，若
⊥
，则θ= ．
| a |
| b |
| a |
| b |
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：根据向量垂直与向量数量积之间的关系，建立方程即可得到结论．
解答：
解：∵向量
=（sinθ，1），
=（1，cosθ），其中0＜θ＜π，
∴若
⊥
，则
•
=0，
即sinθ+cosθ=0，
即tanθ=-1，
∴θ=
，
故答案为：
| a |
| b |
∴若
| a |
| b |
| a |
| b |
即sinθ+cosθ=0，
即tanθ=-1，
∴θ=
| 3π |
| 4 |
故答案为：
| 3π |
| 4 |
点评：本题主要考查平面向量的应用，利用向量垂直与向量数量积之间的关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
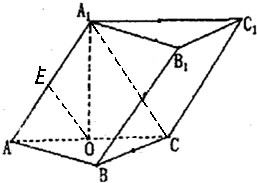如图，三棱柱ABC-A1B1C1中，平面A1ACC1⊥平面ABC，△A1AC，△ABC均为正三角形，点O，E分别为AC，AA1中点．求二面角C1-AB-C的余弦值．