题目内容
20.已知α、β都是锐角,cosα=$\frac{1}{7}$,cos(α+β)=-$\frac{11}{14}$,则tanα=4$\sqrt{3}$,cosβ=$\frac{1}{2}$.分析 利用同角三角函数的基本关系,两角差的三角公式,求得要求式子的值.
解答 解:∵α、β都是锐角,cosα=$\frac{1}{7}$,cos(α+β)=-$\frac{11}{14}$,
∴sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{4\sqrt{3}}{7}$,sin(α+β)=$\sqrt{{1-cos}^{2}(α+β)}$=$\frac{5\sqrt{3}}{14}$,
则tanα=$\frac{sinα}{cosα}$=4$\sqrt{3}$.
cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-$\frac{11}{14}$•$\frac{1}{7}$+$\frac{5\sqrt{3}}{14}$•$\frac{4\sqrt{3}}{7}$=$\frac{49}{98}$=$\frac{1}{2}$,
故答案为:4$\sqrt{3}$;$\frac{1}{2}$.
点评 本题主要考查同角三角函数的基本关系,两角差的三角公式的应用,属于基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
11.cos(π-α)=( )
| A. | cosα | B. | -cosα | C. | sinα | D. | -sinα |
5.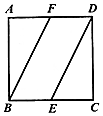 如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )
如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )
 如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )
如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )| A. | 点A与点C在某一位置可能重合 | B. | 点A与点C的最大距离为$\sqrt{3}$AB | ||
| C. | 直线AB与直线CD可能垂直 | D. | 直线AF与直线CE可能垂直 |
12.若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为单位向量,且$\overrightarrow{a}$•$\overrightarrow{b}$=0,($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)≤0,则|$\overrightarrow{a}$+$\overrightarrow{b}$-2$\overrightarrow{c}$|的最大值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |