题目内容
10.设f(x)=asin 2x+bcos 2x,其中a,b∈R,ab≠0.若f(x)≤|f($\frac{π}{6}$)|对一切x∈R恒成立,则以下结论正确的是①②④(写出所有正确结论的编号).①$f(\frac{5π}{12})=0$;
②$|{f(\frac{7π}{12})}$|≥$|{f(\frac{π}{3})}$|;
③f(x)的单调递增区间是(kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$)(k∈Z);
④f(x)既不是奇函数也不是偶函数.
分析 利用辅助角公式化简f(x),根据f(x)≤|f($\frac{π}{6}$)|可得,a,b的值.然后对个结论依次判断即可.
解答 解:由f(x)=asin 2x+bcos 2x=$\sqrt{{a}^{2}+{b}^{2}}$sin(2x+φ).
∵f(x)≤|f($\frac{π}{6}$)|对一切x∈R恒成立
∴当x=$\frac{π}{6}$时,函数取得最大值,即2×$\frac{π}{6}$+φ=$\frac{π}{2}$,解得:φ=$\frac{π}{6}$.
故得f(x)=$\sqrt{{a}^{2}+{b}^{2}}$sin(2x+$\frac{π}{6}$).
则f($\frac{5π}{12}$)=$\sqrt{{a}^{2}+{b}^{2}}$sin(2×$\frac{5π}{12}$+$\frac{π}{6}$)=0,∴①对.
②f($\frac{7π}{12}$)=$\sqrt{{a}^{2}+{b}^{2}}$sin(2×$\frac{7π}{12}$+$\frac{π}{6}$)=$-\sqrt{{a}^{2}+{b}^{2}}$
f($\frac{π}{3}$)=$\sqrt{{a}^{2}+{b}^{2}}$sin(2×$\frac{π}{3}$+$\frac{π}{6}$)=$\frac{1}{2}\sqrt{{a}^{2}+{b}^{2}}$,∴$|{f(\frac{7π}{12})}$|≥$|{f(\frac{π}{3})}$|,∴②对.
由$-\frac{π}{2}+2kπ≤$2x+$\frac{π}{6}$$≤\frac{π}{2}+2kπ$,(k∈Z)
解得:$-\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,(k∈Z)
∴f(x)的单调递增区间是(kπ$-\frac{π}{3}$,kπ+$\frac{π}{6}$)(k∈Z);∴③不对
f(x)的对称轴2x+$\frac{π}{6}$=$\frac{π}{2}$+kπ,(k∈Z);∴③
解得:x=$\frac{1}{2}$kπ+$\frac{π}{6}$,不是偶函数,
当x=0时,f(0)=$\frac{1}{2}$,不关于(0,0)对称,
∴f(x)既不是奇函数也不是偶函数.
故答案为①②④.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,f(x)≤|f($\frac{π}{6}$)|对一切x∈R恒成立,确定φ的一个值时解题的关键,属于中档题.

 阅读快车系列答案
阅读快车系列答案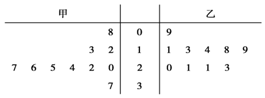 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )| A. | 乙的众数是21 | B. | 甲的中位数是24 | ||
| C. | 甲的极差是29 | D. | 甲罚球命中率比乙高 |
| A. | 在频率分布直方图中,众数左边和右边的直方图的面积相等 | |
| B. | 为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行编号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样 | |
| C. | “x≠1”是“x2-3x+2≠0”的充分不必要条件 | |
| D. | 命题p:“?x0∈R,${x_0}^2-3{x_0}+2<0$”的否定为:“?x∈R,x2-3x+2≥0” |
| A. | (1,$\sqrt{6}$) | B. | (2,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (1,$\sqrt{7}$) |
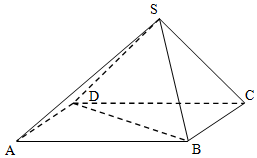 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.