题目内容
5.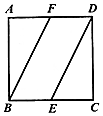 如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )
如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )| A. | 点A与点C在某一位置可能重合 | B. | 点A与点C的最大距离为$\sqrt{3}$AB | ||
| C. | 直线AB与直线CD可能垂直 | D. | 直线AF与直线CE可能垂直 |
分析 当平面ABF⊥平面BEDF,平面DCE⊥平面BEDF时,直线AF与直线CE垂直.
解答 解:在正方形ABCD中,点E,F分别为边BC,AD的中点,
将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,
在翻折的过程中,
在A中,A与C恒不重合,故A错误;
在B中,点A与点C的最大距离为正方形ABCD的对角线AC=$\sqrt{2}AB$,故B不成立;
在C中,直线AB与直线CD不可能垂直,故C不成立;
在D中,当平面ABF⊥平面BEDF,平面DCE⊥平面BEDF时,直线AF与直线CE垂直,故D正确.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15..假设某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料:
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
试求:(1)y与x之间的回归方程;
(2)当使用年限为10年时,估计维修费用是多少?
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
试求:(1)y与x之间的回归方程;
(2)当使用年限为10年时,估计维修费用是多少?
16.2016年初,受国际油价大幅上涨的拉动,一些石油替代型企业生产成本出现大幅度上升,近期,由于国际油价回落,石油替代型企业生产成本明显下降,某PVC行业企业的生产成本在8月份、9月份每月递增20%,国际油价回落之后,10月份、11月份的生产成本每月递减20%,那么该企业在11月底的生产成本与8月初比较( )
| A. | 不增不减 | B. | 约增加5% | C. | 约减少8% | D. | 约减少5% |
13.函数f(x)=$\frac{\sqrt{x-1}}{x-2}$的定义域为( )
| A. | (1,+∞) | B. | [1,+∞) | C. | [1,2) | D. | [1,2)∪(2,+∞) |
10.若函数y=f(x)的图象如图所示,则函数f(x)的解析式可以为( )
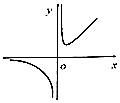

| A. | f(x)=$\frac{{2}^{x}+1}{x}$ | B. | f(x)=$\frac{ln({x}^{2}+2)}{x}$ | C. | f(x)=$\frac{{x}^{3}+3}{x}$ | D. | f(x)=$\frac{lnx}{x}$ |
15.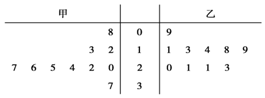 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )| A. | 乙的众数是21 | B. | 甲的中位数是24 | ||
| C. | 甲的极差是29 | D. | 甲罚球命中率比乙高 |
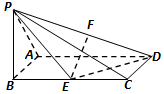 如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.
如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.