题目内容
在锐角△ABC中,角A,B,C对应的边分别是a,b,c.已知2asinB=
b,
(1)求角A的大小;
(2)若△ABC的面积S=5
,b=5,求sinBsinC的值.
| 3 |
(1)求角A的大小;
(2)若△ABC的面积S=5
| 3 |
考点:正弦定理
专题:计算题,解三角形
分析:(1)利用正弦定理把已知等式转化,求得sinA的值,进而求得A.
(2)利用三角形面积公式和已知条件求得c,然后利用余弦定理求得a,进而根据正弦定理求得2R,最后代入sinBsinC的表达式中求得答案.
(2)利用三角形面积公式和已知条件求得c,然后利用余弦定理求得a,进而根据正弦定理求得2R,最后代入sinBsinC的表达式中求得答案.
解答:
解:(1)∵2asinB=
b,
∴2sinAsinB=
sinB,
∴2sinA=
,sinA=
△ABC为锐角三角形,
∴∠A=
(Ⅱ)∵S=
bcsinA=5
∴c=4,
∴a=
=
=
∵(2R)2=
=28
∴sinBsinC=
=
.
| 3 |
∴2sinAsinB=
| 3 |
∴2sinA=
| 3 |
| ||
| 2 |
△ABC为锐角三角形,
∴∠A=
| π |
| 3 |
(Ⅱ)∵S=
| 1 |
| 2 |
| 3 |
∴c=4,
∴a=
| b2+c2-2bccosA |
25+16-2×5×4×
|
| 21 |
∵(2R)2=
| a2 |
| sin2A |
∴sinBsinC=
| bc |
| 4R2 |
| 5 |
| 7 |
点评:本题主要考查了正弦定理和余弦定理的应用.解题的关键是利用正弦定理完成边角问题的转化和化归.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
若实数x,y满足:3x+4y-12=0,则x2+y2+2x的最小值是( )
| A、2 | B、3 | C、5 | D、8 |
已知α终边上在直线y=2x上,则1+sinαcosα等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
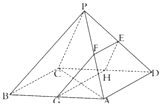 如图,四棱锥P-ABCD中,底面ABCD是边长为2
如图,四棱锥P-ABCD中,底面ABCD是边长为2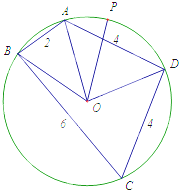 已知圆内接四边形ABCD中,O为圆心,AB=2,BC=6,AD=CD=4.
已知圆内接四边形ABCD中,O为圆心,AB=2,BC=6,AD=CD=4.