题目内容
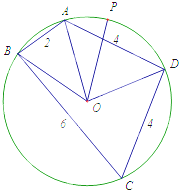已知圆内接四边形ABCD中，O为圆心，AB=2，BC=6，AD=CD=4．（1）求∠BAD的大小和半径AO的长；
（2）若
| AO |
| AB |
| AD |
（3）若P是弧BAD上的动点，
| OP |
| OB |
| OD |
考点：余弦定理
专题：解三角形
分析：（1）连结BD，在△ABD和△CBD中，通过余弦定理可得∠BAD的大小，利用正弦定理即可求解半径AO的长；
（2）以O为坐标原点，OD所在直线为x轴，建立直角坐标系，利用
=x
+y
，列出方程组即可求x+y的值；
（3）设P（Rcosθ，Rsinθ），利用
=λ
+μ
，求出λ+μ的表达式，利用三角函数的值域求解其最大值和最小值．
（2）以O为坐标原点，OD所在直线为x轴，建立直角坐标系，利用
| AO |
| AB |
| AD |
（3）设P（Rcosθ，Rsinθ），利用
| OP |
| OB |
| OD |
解答：
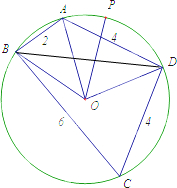解：（1）连结BD，在△ABD和△CBD中，
由余弦定理可得：
BD2=AB2+AD2-2AD•ABcos∠BAD=4+16-16cos∠BAD，
BD2=CB2+CD2-2CD•CBcos∠BCD=36+16+cos∠BAD，
∴4+16-16cos∠BAD=36+16+cos∠BAD
∴cos∠BAD=-
，
∴∠BAD=120°．
从而BD=2
，AO=
=
．
（2）在三角形AOD中，由余弦定理可知：cos∠AOD=
＞0，sin∠AOD=
，
以O为坐标原点，OD所在直线为x轴，建立直角坐标系，
则D(
，0)，A(
，
)，B(-
，
)，
由
=x
+y
，
得
得x=-
，y=-
，
x+y=-8．
（3）设P（Rcosθ，Rsinθ），θ∈[0，
]，
由
=λ
+μ
，
得
∴λ+μ=
sinθ+cosθ=2sin(θ+
)
∵θ∈[0，
]
∴（λ+μ）max=2，（λ+μ）min=1．
解：（1）连结BD，在△ABD和△CBD中，由余弦定理可得：
BD2=AB2+AD2-2AD•ABcos∠BAD=4+16-16cos∠BAD，
BD2=CB2+CD2-2CD•CBcos∠BCD=36+16+cos∠BAD，
∴4+16-16cos∠BAD=36+16+cos∠BAD
∴cos∠BAD=-
| 1 |
| 2 |
∴∠BAD=120°．
从而BD=2
| 7 |
| ||
| sin120° |
2
| ||
| 3 |
（2）在三角形AOD中，由余弦定理可知：cos∠AOD=
| 1 |
| 7 |
4
| ||
| 7 |
以O为坐标原点，OD所在直线为x轴，建立直角坐标系，
则D(
2
| ||
| 3 |
2
| ||
| 21 |
8
| ||
| 7 |
| ||
| 3 |
| 7 |
由
| AO |
| AB |
| AD |
得
|
得x=-
| 94 |
| 21 |
| 74 |
| 21 |
x+y=-8．
（3）设P（Rcosθ，Rsinθ），θ∈[0，
| 2π |
| 3 |
由
| OP |
| OB |
| OD |
得
|
∴λ+μ=
2
| ||
| 3 |
| π |
| 6 |
∵θ∈[0，
| 2π |
| 3 |
∴（λ+μ）max=2，（λ+μ）min=1．
点评：本题考查余弦定理以及正弦定理向量的相等关系的应用，三角函数的化简求值，考查转化思想以及计算能力．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目