题目内容
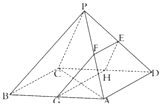 如图,四棱锥P-ABCD中,底面ABCD是边长为2
如图,四棱锥P-ABCD中,底面ABCD是边长为2| 2 |
| 5 |
(Ⅰ)证明:EF∥平面ABCD;
(Ⅱ)求截面EFGH与平面PAD所成锐二面角的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间角
分析:(Ⅰ)由已知条件推导出EH∥PC,EF∥AD,由此能证明EF∥平面ABCD.
(Ⅱ)设AC∩BD=O,以O为原点,OB,OA,OP分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出截面EFGH与平面PAD所成锐二面角的余弦值.
(Ⅱ)设AC∩BD=O,以O为原点,OB,OA,OP分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出截面EFGH与平面PAD所成锐二面角的余弦值.
解答:
(Ⅰ)证明:∵平面EFGH∥平面PBC,
平面EFGH∩平面PCD=EH,平面PBC∩平面PCD=PC,
∴EH∥PC,又E是PD的中点,∴H是CD的中点,
同理可证F,G分别是PA、AB的中点,
∴EF∥AD,又EF不包含于平面ABCD,AD?平面ABCD,
∴EF∥平面ABCD.
(Ⅱ)解:∵底面ABCD是边长为2
的正方形,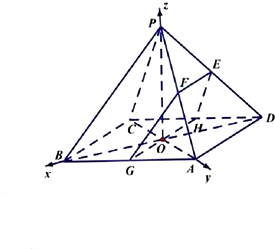
设AC∩BD=O,则AC⊥BD,且AC=BD=4,
由侧面侧棱长为
的等腰三角形,知:
PO⊥AC,PO⊥BD,∴PO⊥平面ABCD,
∴以O为原点,OB,OA,OP分别为x轴,y轴,z轴,建立空间直角坐标系,
由题意知A(0,2,0),B(2,0,0),
C(0,-2,0),D(-2,0,0),P(0,0,1),
由平面EFGH∥平面PBC知平面EFGH与平面PAD所成锐二面角等于平面PBC与平面PAD所成锐二面角,
设平面PBC的法向量为
=(x,y,z),
∵
=(2,0,-1),
=(0,-2,-1),
∴
,
取x=1,得
=(1,-1,2).
设平面PAD的法向量
=(x1,y1,z1),
∵
=(0,2,-1),
=(-2,0,-1),
∴
,
取x1=1,得
=(1,-1,-2),
设截面EFGH与平面PAD所成锐二面角的平面角为θ,
则cosθ=|cos<
,
>|=|
|=
,
∴截面EFGH与平面PAD所成锐二面角的余弦值为
.
平面EFGH∩平面PCD=EH,平面PBC∩平面PCD=PC,
∴EH∥PC,又E是PD的中点,∴H是CD的中点,
同理可证F,G分别是PA、AB的中点,
∴EF∥AD,又EF不包含于平面ABCD,AD?平面ABCD,
∴EF∥平面ABCD.
(Ⅱ)解:∵底面ABCD是边长为2
| 2 |

设AC∩BD=O,则AC⊥BD,且AC=BD=4,
由侧面侧棱长为
| 5 |
PO⊥AC,PO⊥BD,∴PO⊥平面ABCD,
∴以O为原点,OB,OA,OP分别为x轴,y轴,z轴,建立空间直角坐标系,
由题意知A(0,2,0),B(2,0,0),
C(0,-2,0),D(-2,0,0),P(0,0,1),
由平面EFGH∥平面PBC知平面EFGH与平面PAD所成锐二面角等于平面PBC与平面PAD所成锐二面角,
设平面PBC的法向量为
| m |
∵
| PB |
| PC |
∴
|
取x=1,得
| m |
设平面PAD的法向量
| n |
∵
| PA |
| PD |
∴
|
取x1=1,得
| n |
设截面EFGH与平面PAD所成锐二面角的平面角为θ,
则cosθ=|cos<
| m |
| n |
| -2 | ||||
|
| 1 |
| 3 |
∴截面EFGH与平面PAD所成锐二面角的余弦值为
| 1 |
| 3 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
甲乙两人进行羽毛球比赛,比赛采取五局三胜制,无论哪一方先胜三局则比赛结束,假定甲每局比赛获胜的概率均为
,则甲以3:1的比分获胜的概率为( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
以下程序运行结果为( )
t=1
For i=2 To 5
t=t*i
Next
输出t.
t=1
For i=2 To 5
t=t*i
Next
输出t.
| A、80 | B、95 |
| C、100 | D、120 |
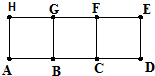 已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.
已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.