题目内容
已知函数f(x)=x3-ax2-a2x,其中a≥0.
(1)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)在区间[0,2]上的最小值g(a).
(1)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)在区间[0,2]上的最小值g(a).
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)把a=2代入函数解析式,求出函数的导函数,进一步求出f(1)和f′(1),由直线方程的点斜式得到曲线y=f(x)在点(1,f(1))处的切线方程;
(2)由导数求出函数在区间(0,2)上的极值,和端点值比较后得函数f(x)在区间[0,2]上的最小值.
(2)由导数求出函数在区间(0,2)上的极值,和端点值比较后得函数f(x)在区间[0,2]上的最小值.
解答:
解:(1)当a=2时,函数f(x)=x3-2x2-4x,
∴f'(x)=3x2-4x-4,
∴f'(1)=-5,f(1)=-5,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y+5=-5×(x-1),
即5x+y=0;
(2)x∈[0,2],f'(x)=3x2-2ax-a2=(x-a)(3x+a),
令f'(x)=0,则x1=-
,x2=a.
①当a=0时,f'(x)=3x2≥0在[0,2]上恒成立,
∴函数f(x)在区间[0,2]上单调递增,∴f(x)min=f(0)=0;
②当0<a<2时,在区间[0,a)上,f'(x)<0,在区间(a,2]上,f'(x)>0,
∴函数f(x)在区间[0,a)上单调递减,在区间(a,2]上单调递增,且x=a是[0,2]上唯一极值点,
∴f(x)min=f(a)=-a3;
③当a≥2时,在区间[0,2]上,f'(x)≤0(仅有当a=2时f'(2)=0),
∴f(x)在区间[0,2]上单调递减,∴函数f(x)min=f(2)=8-4a-2a2.
综上所述,当0≤a<2时,函数f(x)的最小值为-a3,a≥2时,函数f(x)的最小值为8-4a-2a2.
故g(a)=
.
∴f'(x)=3x2-4x-4,
∴f'(1)=-5,f(1)=-5,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y+5=-5×(x-1),
即5x+y=0;
(2)x∈[0,2],f'(x)=3x2-2ax-a2=(x-a)(3x+a),
令f'(x)=0,则x1=-
| a |
| 3 |
①当a=0时,f'(x)=3x2≥0在[0,2]上恒成立,
∴函数f(x)在区间[0,2]上单调递增,∴f(x)min=f(0)=0;
②当0<a<2时,在区间[0,a)上,f'(x)<0,在区间(a,2]上,f'(x)>0,
∴函数f(x)在区间[0,a)上单调递减,在区间(a,2]上单调递增,且x=a是[0,2]上唯一极值点,
∴f(x)min=f(a)=-a3;
③当a≥2时,在区间[0,2]上,f'(x)≤0(仅有当a=2时f'(2)=0),
∴f(x)在区间[0,2]上单调递减,∴函数f(x)min=f(2)=8-4a-2a2.
综上所述,当0≤a<2时,函数f(x)的最小值为-a3,a≥2时,函数f(x)的最小值为8-4a-2a2.
故g(a)=
|
点评:本题考查了利用导数研究曲线上某点处的切线方程,考查了利用导数求函数的最值,体现了分类讨论的数学思想方法.是压轴题.

练习册系列答案
相关题目
执行如图所示的程序图,则输出的n为( )


| A、3 | B、4 | C、5 | D、6 |
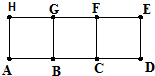 已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.
已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.