题目内容
已知函数f(x)=|x+1|.
(1)作出函数f(x)的图象;
(2)写出函数的单调区间.
(1)作出函数f(x)的图象;
(2)写出函数的单调区间.
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:(1)利用分段函数,分当x≥-1,x<-1两种情况,作出相应的图象;
(2)根据图象即可写出函数的单调区间.
(2)根据图象即可写出函数的单调区间.
解答:
解:(1)∵f(x)=|x+1|,
∴f(x)=
则函数图象如图所示:

(2)由图象可知,f(x)在[-1,+∞)上单调递增,在(-∞,-1)上单调递减.
∴f(x)=
|
则函数图象如图所示:

(2)由图象可知,f(x)在[-1,+∞)上单调递增,在(-∞,-1)上单调递减.
点评:本题考查了函数图象的作法和单调区间的求法,属于基础题.

练习册系列答案
相关题目
在等比数列{an}中,Sn是它的前n项和,若a2•a3=2a1,且a4与2a7的等差中项为17,则S6=( )
A、
| ||
| B、16 | ||
| C、15 | ||
D、
|
已知cosαcosβ=
,sin(
+α+β)=
,则sinαsinβ=( )
| 1 |
| 3 |
| π |
| 2 |
| 7 |
| 8 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
以下程序运行结果为( )
t=1
For i=2 To 5
t=t*i
Next
输出t.
t=1
For i=2 To 5
t=t*i
Next
输出t.
| A、80 | B、95 |
| C、100 | D、120 |
要得到一个偶函数的图象,只需将函数f(x)=sin(x-
)的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
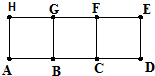 已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.
已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.