题目内容
已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=x2+2x,若存在实数a,b(0<a<b),使f(x)在[a,b]上的值域是[
,
].则b-a的最小值是( )
| 1 |
| b |
| 1 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:先由奇函数的性质和题意,求得x>0时f(x)的解析式,对于正实数a、b,分三种情况讨论:①、当a<1<b时,②、当a<b<1时,③、当1≤a<b时,结合二次函数的性质,分析可得a、b的值,将其相减可得答案.
解答:
解:设x>0,则-x<0,
代入当x<0时f(x)=x2+2x,得f(-x)=-2x+x2,
又y=f(x)是定义在R上的奇函数,所以f(-x)=-f(x),
则x>0时,f(x)=2x-x2,且对称轴x=1,
所以,对于a、b分三种情况讨论:
①、当0<a<1<b时,f(x)=2x-x2的最大值为1,得
=1,
即a=1,不合题意,舍去,
②、当0<a<b<1时,f(a)<1,f(b)<1且在[a,b]上单调增,
而
>1,不合题意,舍去,
③、当1≤a<b时,f(x)在[a,b]上单调减,
可得
,解得a=1,b=
,
则b-a=
,
故选:B.
代入当x<0时f(x)=x2+2x,得f(-x)=-2x+x2,
又y=f(x)是定义在R上的奇函数,所以f(-x)=-f(x),
则x>0时,f(x)=2x-x2,且对称轴x=1,
所以,对于a、b分三种情况讨论:
①、当0<a<1<b时,f(x)=2x-x2的最大值为1,得
| 1 |
| a |
即a=1,不合题意,舍去,
②、当0<a<b<1时,f(a)<1,f(b)<1且在[a,b]上单调增,
而
| 1 |
| a |
③、当1≤a<b时,f(x)在[a,b]上单调减,
可得
|
1+
| ||
| 2 |
则b-a=
| ||
| 2 |
故选:B.
点评:本题考查了函数的奇偶性与单调性,函数的解析式求法,二次函数的性质,考查了分类讨论的数学思想,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知复数z1=2+ai(a∈R),z2=1-2i,若
为纯虚数,则|z1|=( )
| z1 |
| z2 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
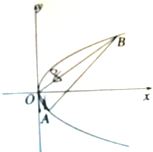 如图,已知抛物线有一个内接直角三角形,直角顶点在原点,两直角边分别为1和8,求抛物线方程.
如图,已知抛物线有一个内接直角三角形,直角顶点在原点,两直角边分别为1和8,求抛物线方程.