题目内容
如图，平面α、β、r两两相交，a、b、c为三条交线，且a∥b，问：a与c，b与c之间有什么关系．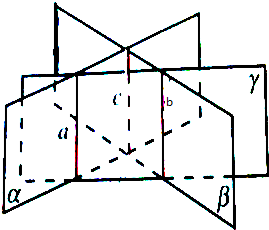
考点：平面与平面之间的位置关系
专题：空间位置关系与距离
分析：得出结论a∥c，b∥c；利用直线与平面平行的判断定理与性质定理，即可证明结论成立．
解答：
解：a∥c，b∥c；
证明如下：
∵α∩γ=a，β∩γ=b，
∴a?β，b?β，
又∵a∥b，
∴a∥β；
又∵α∩β=c，
a?α，
∴a∥c；
同理b∥c．
证明如下：
∵α∩γ=a，β∩γ=b，
∴a?β，b?β，
又∵a∥b，
∴a∥β；
又∵α∩β=c，
a?α，
∴a∥c；
同理b∥c．
点评：本题考查了直线与平面平行的判断定理与性质定理的应用问题，也考查了几何语言与图形语言以及符号语言的应用问题，是基础题．
练习册系列答案
相关题目
函数f（x）=lg（3x+1）的定义域是（ ）
A、（-
| ||||
B、（-
| ||||
C、（-
| ||||
D、（-∞，-
|
如图，已知正六棱柱的最大对角面的面积为4m2，互相平行的两个侧面的距离为2m，则这个六棱柱的体积为
如图，设椭圆已知函数f（x）是定义在R上的奇函数，当x＜0时，f（x）=x2+2x，若存在实数a，b（0＜a＜b），使f（x）在[a，b]上的值域是[
，
]．则b-a的最小值是（ ）
| 1 |
| b |
| 1 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|