题目内容
画出下列函数的图象,并写出它的定义域、值域、单调区间、最大最小值.
(1)y=2|x|-1;
(2)y=|2x-1|;
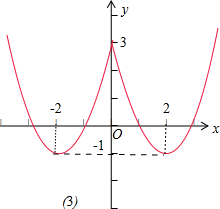
(3)y=x2-4|x|+3;
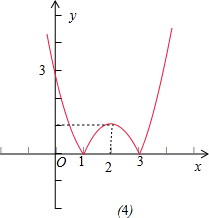
(4)y=|x2-4x+3|.
(1)y=2|x|-1;
(2)y=|2x-1|;
(3)y=x2-4|x|+3;
(4)y=|x2-4x+3|.
考点:函数的单调性及单调区间,函数的值域
专题:函数的性质及应用
分析:根据函数的解析式画出各个函数的图象,数形结合求得各个函数的定义域、值域、单调区间、最大最小值.
解答:
解:先根据函数的解析式画出各个函数的图象,如图所示:
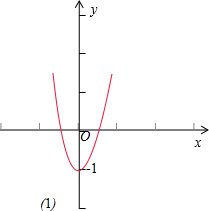
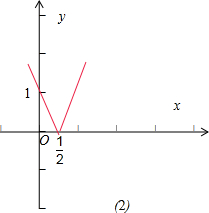
故(1)函数y=2|x|-1 的定义域为R;值域为[-1,+∞);单调增区间为[0,+∞)、减区间为(-∞,0);无最大最,最小值为-1.
(2)函数y=|2x-1|的定义域为R;值域为[0,+∞);单调增区间为[
,+∞)、减区间为(-∞,
);无最大最,最小值为0.
(3)函数y=x2-4|x|+3的定义域为R;值域为[-1,+∞);单调增区间为[-2,0]、[2,+∞);减区间为(-∞,-2)、(0,2);无最大最,最小值为-1.
(4)y=|x2-4x+3|的定义域为R;值域为[0,+∞);单调增区间为[3,+∞)、[1,2];减区间为(-∞,1)、(2,3);无最大最,最小值为.
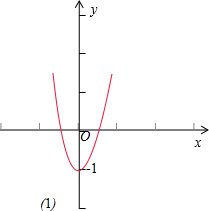
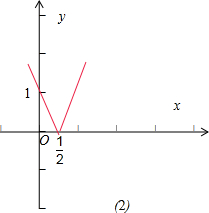


故(1)函数y=2|x|-1 的定义域为R;值域为[-1,+∞);单调增区间为[0,+∞)、减区间为(-∞,0);无最大最,最小值为-1.
(2)函数y=|2x-1|的定义域为R;值域为[0,+∞);单调增区间为[
| 1 |
| 2 |
| 1 |
| 2 |
(3)函数y=x2-4|x|+3的定义域为R;值域为[-1,+∞);单调增区间为[-2,0]、[2,+∞);减区间为(-∞,-2)、(0,2);无最大最,最小值为-1.
(4)y=|x2-4x+3|的定义域为R;值域为[0,+∞);单调增区间为[3,+∞)、[1,2];减区间为(-∞,1)、(2,3);无最大最,最小值为.
点评:本题主要考查带有绝对值的函数的图象、性质,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=x2+2x,若存在实数a,b(0<a<b),使f(x)在[a,b]上的值域是[
,
].则b-a的最小值是( )
| 1 |
| b |
| 1 |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在数列{an}中,a1=1,an+1-an=2则a51的值为( )
| A、49 | B、99 |
| C、101 | D、102 |