题目内容
已知在同一直角坐标系中,函数f(x)=m2x2+4mx和函数g(x)=x2+4x-3的图象与直线x=a分别交于M、N两点,若对于任意实数a,点M始终比点N高,求m的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:由题意得不等式,根据二次函数的性质,从而求出m的范围.
解答:
解:显然m≠0,
由题意得:m2a2+4ma>a2+4a-3,
∴(m2-1)a2+(4m-4)a+3>对于任意实数a恒成立,
∴m2-1≠0
∴△=(4m-4)2-12(m2-1)<0,解得:-1<m<1,
∴m的范围是:(-1,1).
由题意得:m2a2+4ma>a2+4a-3,
∴(m2-1)a2+(4m-4)a+3>对于任意实数a恒成立,
∴m2-1≠0
∴△=(4m-4)2-12(m2-1)<0,解得:-1<m<1,
∴m的范围是:(-1,1).
点评:本题考查了二次函数的性质,函数恒成立问题,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列关于函数f(x)=(x+1)|x|的单调性的叙述中,正确的是( )
| A、f(x)在定义域上单调递增 | ||
| B、f(x)在定义域上单调递减 | ||
| C、f(x)在(-∞,0)上是增函数,在(0,+∞)上是减函数 | ||
D、f(x)在(-
|
当a>0时,函数f(x)=(x2-ax)ex的图象大致是( )
A、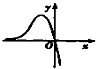 |
B、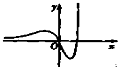 |
C、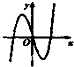 |
D、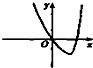 |
函数f(x)=4lnx-x2的大致图象是( )
A、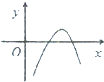 |
B、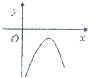 |
C、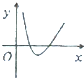 |
D、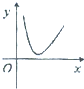 |