题目内容
若不等式|x|<1成立时,不等式1<x-a<4也成立,求实数a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:求出不等式|x|<1和1<x-a<4的解集,根据不等式之间的关系建立不等式解集之间的关系,即可得到所求.
解答:
解:不等式[x-(a+1)][x-(a+4)]<0,
∵|x|<1,∴-1<x<1,
∵1<x-a<4,∴a+1<x<a+4,
∵不等式|x|<1成立,则不等式1<x-a<4也成立,
∴{x|-1<x<1}⊆{x|a+1<x<a+4},
即
,
解得
,
∴-3≤a≤-2,
即实数a的取值范围是[-3,-2].
∵|x|<1,∴-1<x<1,
∵1<x-a<4,∴a+1<x<a+4,
∵不等式|x|<1成立,则不等式1<x-a<4也成立,
∴{x|-1<x<1}⊆{x|a+1<x<a+4},
即
|
解得
|
∴-3≤a≤-2,
即实数a的取值范围是[-3,-2].
点评:本题注意考查不等式的解法以及不等式恒成立,将不等式转化为不等式解集之间的关系是解决本题的根据.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
(文)若a∈R,则“a2>a”是“a>1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
如图所示,网格纸上小正方形的边长为1cm,粗实线为某空间几何体的三视图,则该几何体的体积为( )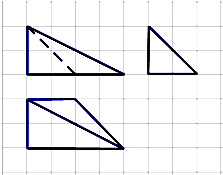

| A、2cm3 |
| B、4cm3 |
| C、6cm3 |
| D、8cm3 |
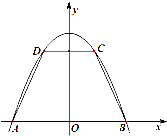 如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.
如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.