题目内容
已知数列{an}满足:a1=1,a2=a(a>0),数列{bn}满足:bn=anan+2(n∈N*)
(1)若数列{an}是等差数列,且b3=45,求a的值及数列{an}通项公式;
(2)若数列{an}的等比数列,求数列{bn}的前n项和Sn.
(1)若数列{an}是等差数列,且b3=45,求a的值及数列{an}通项公式;
(2)若数列{an}的等比数列,求数列{bn}的前n项和Sn.
考点:数列的求和,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)先根据{an}是等差数列表示出通项公式,再根据b3=45求得a3a5的值从而可确定a的值,求得{an}的通项公式.
(2)先根据{an}是等比数列表示出通项公式,进而可表示出bn的表达式,再对公比a等于1和不等于1进行讨论,即可得到最后答案.
(2)先根据{an}是等比数列表示出通项公式,进而可表示出bn的表达式,再对公比a等于1和不等于1进行讨论,即可得到最后答案.
解答:
解:(1)∵{an}是等差数列,a1=1,a2=a(a>0),∴an=1+(n-1)(a-1).
又b3=45,∴a3a5=45,即(2a-1)(4a-3)=45,
解得a=2或a=-
(舍去),…(5分)
∴an=2n-1.…(7分)
(2))∵{an}是等比数列,a1=1,a2=a(a>0),∴an=an-1,则bn=anan+2=a2n.
∴当a=1时,Sn=n;
当a≠1时,Sn=
.…(14分)
又b3=45,∴a3a5=45,即(2a-1)(4a-3)=45,
解得a=2或a=-
| 7 |
| 4 |
∴an=2n-1.…(7分)
(2))∵{an}是等比数列,a1=1,a2=a(a>0),∴an=an-1,则bn=anan+2=a2n.
∴当a=1时,Sn=n;
当a≠1时,Sn=
| a2(1-a2n) |
| 1-a2 |
点评:本题主要考查数列的通项公式的求法和数列求和.高考对数列的考查无外乎通项公式的求法和前n项和的求法,对经常用到的常用方法要熟练掌握.

练习册系列答案
相关题目
方程x2+y2+2ax+2by+a2+b2=0表示的图形是( )
| A、以(a,b)为圆心的圆 |
| B、以(-a,-b)为圆心的圆 |
| C、点(a,b) |
| D、点(-a,-b) |
如图所示,网格纸上小正方形的边长为1cm,粗实线为某空间几何体的三视图,则该几何体的体积为( )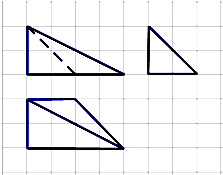

| A、2cm3 |
| B、4cm3 |
| C、6cm3 |
| D、8cm3 |
设m、n是两条不同的直线,α、β是两个不同的平面,下列命题中错误的是( )
| A、若m⊥α,m∥n,n∥β,则α⊥β |
| B、若α⊥β,m?α,m⊥β,则m∥α |
| C、若m⊥β,m?α,则α⊥β |
| D、若α⊥β,m?α,n?β,则m⊥n |
设p:x∈R,q:2<x<3,则p是q成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |