Question

函数f（x）=4lnx-x²的大致图象是（　　）

• A、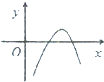
• B、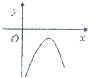
• C、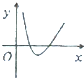
• D、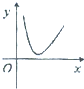

Answer 1

考点：函数的图象

专题：函数的性质及应用

分析：先求导，从而可求得函数f（x）=4lnx-x²的单调区间与极值，问题即可解决．

解答： 解：∵f（x）=4lnx-x²，其定义域为（0，+∞）
∴f′（x）=

4

x

-2x=

2(2-x2)

x

由f′（x）＞0得，0＜x＜

2

；f′（x）＜0得，x＞

2

；
∴f（x）=4lnx-x²，在（0，

2

）上单调递增，在（

2

，+∞）上单调递减；
∴x=

2

时，f（x）取到极大值．又f（

2

）=2（ln2-1）＜0，
∴函数f（x）=4lnx-x²的图象在x轴下方，可排除A，C，D．
故选：B．

点评：本题考查函数的图象，是以考查函数的图象为载体考查导数及其应用，注重考查学生分析转化解决问题的能力，属于基础题．