题目内容
10. 已知某四棱锥的三视图(单位:cm)如图所示,则该几何体的体积是$\frac{8\sqrt{3}}{3}$,其全面积是16+$\sqrt{3}$+$\sqrt{19}$.
已知某四棱锥的三视图(单位:cm)如图所示,则该几何体的体积是$\frac{8\sqrt{3}}{3}$,其全面积是16+$\sqrt{3}$+$\sqrt{19}$.
分析 根据四棱锥的三视图知四棱锥是侧放的直四棱锥,
结合题意画出该四棱锥的直观图,计算它的体积和全面积.
解答 解:根据四棱锥的三视图知,则四棱锥是侧放的直四棱锥,
且底面四边形是矩形,边长分别为4和2,高为$\sqrt{3}$,如图所示;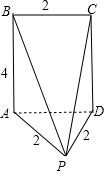
所以该四棱锥的体积为
V四棱锥=$\frac{1}{3}$×4×2×$\sqrt{3}$=$\frac{8\sqrt{3}}{3}$;
其全面积为S=2×4+2×$\frac{1}{2}$×2×4+$\frac{1}{2}$×2×$\sqrt{3}$+$\frac{1}{2}$×2×$\sqrt{{4}^{2}{+(\sqrt{3})}^{2}}$=16+$\sqrt{3}$+$\sqrt{19}$.
故答案为:$\frac{8\sqrt{3}}{3}$,16+$\sqrt{3}$+$\sqrt{19}$.
点评 本题考查了空间几何体三视图的应用问题,是基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
1. 如图,D、E、F分别是△ABC的边AB、BC、CA的中点,则下列等式中错误的是( )
如图,D、E、F分别是△ABC的边AB、BC、CA的中点,则下列等式中错误的是( )
 如图,D、E、F分别是△ABC的边AB、BC、CA的中点,则下列等式中错误的是( )
如图,D、E、F分别是△ABC的边AB、BC、CA的中点,则下列等式中错误的是( )| A. | $\overrightarrow{FD}$+$\overrightarrow{DA}$+$\overrightarrow{DE}$=0 | B. | $\overrightarrow{AD}$+$\overrightarrow{BE}$+$\overrightarrow{CF}$=0 | C. | $\overrightarrow{FD}$+$\overrightarrow{DE}$+$\overrightarrow{AD}$=$\overrightarrow{AB}$ | D. | $\overrightarrow{AD}$+$\overrightarrow{EC}$+$\overrightarrow{FD}$=$\overrightarrow{BD}$ |
5. 一光源P在桌面A的正上方,半径为2的球与桌面相切,且PA与球相切,小球在光源P的中心投影下在桌面产生的投影为一椭圆,如图所示,形成一个空间几何体,且正视图是Rt△PAB,其中PA=6,则该椭圆的长轴长为( )
一光源P在桌面A的正上方,半径为2的球与桌面相切,且PA与球相切,小球在光源P的中心投影下在桌面产生的投影为一椭圆,如图所示,形成一个空间几何体,且正视图是Rt△PAB,其中PA=6,则该椭圆的长轴长为( )
 一光源P在桌面A的正上方,半径为2的球与桌面相切,且PA与球相切,小球在光源P的中心投影下在桌面产生的投影为一椭圆,如图所示,形成一个空间几何体,且正视图是Rt△PAB,其中PA=6,则该椭圆的长轴长为( )
一光源P在桌面A的正上方,半径为2的球与桌面相切,且PA与球相切,小球在光源P的中心投影下在桌面产生的投影为一椭圆,如图所示,形成一个空间几何体,且正视图是Rt△PAB,其中PA=6,则该椭圆的长轴长为( )| A. | 6 | B. | 8 | C. | $4\sqrt{3}$ | D. | 3 |
2.sin72°cos12°-cos72°sin12°的值为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
19.从10名学生中选3名组成一组,则甲、乙至少有1人入选,而丙没有入选的不同选法种数为( )
| A. | 42 | B. | 56 | C. | 49 | D. | 28 |
20.已知函数f(x)=(${\sqrt{3}$cosx-sinx)(cosx+$\sqrt{3}$sinx),则下面结论中错误的是( )
| A. | 函数f(x)的最小正周期为π | |
| B. | 函数f(x)的图象关于直线$x=\frac{π}{12}$对称 | |
| C. | 函数f(x)的图象可由g(x)=2sin2x的图象向右平移$\frac{π}{6}$个单位得到 | |
| D. | 函数f(x)在区间$[{-\frac{π}{4},0}]$上是增函数 |