题目内容
20.已知函数f(x)=(${\sqrt{3}$cosx-sinx)(cosx+$\sqrt{3}$sinx),则下面结论中错误的是( )| A. | 函数f(x)的最小正周期为π | |
| B. | 函数f(x)的图象关于直线$x=\frac{π}{12}$对称 | |
| C. | 函数f(x)的图象可由g(x)=2sin2x的图象向右平移$\frac{π}{6}$个单位得到 | |
| D. | 函数f(x)在区间$[{-\frac{π}{4},0}]$上是增函数 |
分析 将f(x)化简,结合三角函数的性质求解即可.
解答 解:函数$f(x)=({\sqrt{3}cosx-sinx})({cosx+\sqrt{3}sinx})$,
化简可得:f(x)=$\sqrt{3}$cos2x+3sinxcosx-sinxcosx-$\sqrt{3}$sin2x=$\sqrt{3}$cos2x+sin2x=2sin(2x+$\frac{π}{3}$)
最小正周期T=$\frac{2π}{2}=π$.∴A对.
令x=$\frac{π}{12}$,即f($\frac{π}{12}$)=2sin($\frac{π}{2}$)=2,∴关于直线$x=\frac{π}{12}$对称,B对.
函数g(x)=2sin2x的图象向右平移$\frac{π}{6}$个单位,可得:2sin2(x-$\frac{π}{6}$)=2sin(2x-$\frac{π}{3}$)≠f(x),∴C不对.
令$-\frac{π}{2}≤$2x+$\frac{π}{3}$≤$\frac{π}{2}$上单调递增,可得:$-\frac{5π}{12}≤x≤\frac{π}{12}$,∴函数f(x)在区间$[{-\frac{π}{4},0}]$上是增函数,∴D对.
故选:C.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 已知某四棱锥的三视图(单位:cm)如图所示,则该几何体的体积是$\frac{8\sqrt{3}}{3}$,其全面积是16+$\sqrt{3}$+$\sqrt{19}$.
已知某四棱锥的三视图(单位:cm)如图所示,则该几何体的体积是$\frac{8\sqrt{3}}{3}$,其全面积是16+$\sqrt{3}$+$\sqrt{19}$.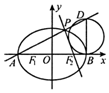 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,左、右焦点为F1,F2,点M为椭圆C上的任意一点,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,左、右焦点为F1,F2,点M为椭圆C上的任意一点,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值为2.