题目内容
5.已知数列{an}的前n项和${A_n}={n^2}({n∈{N^*}}),{b_n}=\frac{a_n}{{{a_{n+1}}}}+\frac{{{a_{n+1}}}}{a_n}({n∈{N^*}})$,数列{bn}的前n项和为Bn.(1)求数列{an}的通项公式;
(2)设${c_n}=\frac{a_n}{2^n}({n∈{N^*}})$,求数列{cn}的前n项和Cn;
(3)证明:$2n<{B_n}<2n+2({n∈{N^*}})$.
分析 (1)当n≥2时,利用an=An-An-1可得an=2n-1,再验证n=1的情况,即可求得数列{an}的通项公式;
(2)由题意知:${c_n}=\frac{a_n}{2^n}=\frac{2n-1}{2^n}$,利用错位相减法即可求得数列{cn}的前n项和Cn;
(3)利用基本不等式可得${b_n}=\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}$>$2\sqrt{\frac{2n-1}{2n+1}•\frac{2n+1}{2n-1}}=2$,可得Bn=b1+b2+…+bn>2n;再由bn=$\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}=1-\frac{2}{2n+1}+1+\frac{2}{2n-1}=2+\frac{2}{2n-1}-\frac{2}{2n+1}$,累加可${B_n}=(2+\frac{2}{1}-\frac{2}{3})+(2+\frac{2}{3}-\frac{2}{5})+…+(2+\frac{2}{2n-1}-\frac{2}{2n+1})=2n+2-\frac{2}{2n+1}<2n+2$,
于是可证明:$2n<{B_n}<2n+2({n∈{N^*}})$.
解答 (本小题满分13分)
解:( I)当n≥2时,${A_n}={n^2}$,${A_{n-1}}={(n-1)^2}$,
两式相减:an=An-An-1=2n-1;
当n=1时,a1=A1=1,也适合an=2n-1,
故数列{an}的通项公式为an=2n-1;.…(3分)
( II)由题意知:${c_n}=\frac{a_n}{2^n}=\frac{2n-1}{2^n}$,Cn=c1+c2+…+cn,
${C_n}=\frac{1}{2^1}+\frac{3}{2^2}+\frac{5}{2^3}+…+\frac{2n-1}{2^n}$,$\frac{C_n}{2}=\frac{1}{2^2}+\frac{3}{2^3}+\frac{5}{2^4}+…+\frac{2n-1}{{{2^{n+1}}}}$,
两式相减可得:$\frac{C_n}{2}=\frac{1}{2^1}+\frac{2}{2^2}+\frac{2}{2^3}+…+\frac{2}{2^n}-\frac{2n-1}{{{2^{n+1}}}}$,…(4分)
即$\frac{C_n}{2}=\frac{1}{2}+(\frac{1}{2^1}+\frac{1}{2^2}+\frac{1}{2^3}+…+\frac{1}{{{2^{n-1}}}})-\frac{2n-1}{{{2^{n+1}}}}$,$\frac{C_n}{2}=\frac{1}{2}+(1-\frac{1}{{{2^{n-1}}}})-\frac{2n-1}{{{2^{n+1}}}}$,${C_n}=3-\frac{2n+3}{2^n}$.…(7分)
( III)${b_n}=\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}$,显然$\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}>2\sqrt{\frac{2n-1}{2n+1}•\frac{2n+1}{2n-1}}=2$,
即bn>2,Bn=b1+b2+…+bn>2n; …(9分)
另一方面,$\frac{2n-1}{2n+1}+\frac{2n+1}{2n-1}=1-\frac{2}{2n+1}+1+\frac{2}{2n-1}=2+\frac{2}{2n-1}-\frac{2}{2n+1}$,
即${b_1}=2+\frac{2}{1}-\frac{2}{3}$,${b_2}=2+\frac{2}{3}-\frac{2}{5}$,…,${b_n}=2+2({\frac{1}{2n-1}-\frac{1}{2n+1}})$,${B_n}=(2+\frac{2}{1}-\frac{2}{3})+(2+\frac{2}{3}-\frac{2}{5})+…+(2+\frac{2}{2n-1}-\frac{2}{2n+1})=2n+2-\frac{2}{2n+1}<2n+2$,
即:2n<Bn<2n+2.…(13分)
点评 本题考查数列递推式的应用,突出考查错位相减法求和与累加法求和的综合运用,考查推理与运算能力,属于难题.

| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
| A. | f(x)是奇函数,则在(0,+∞)上是增函数 | |
| B. | f(x)是偶函数,则在(0,+∞)上是减函数 | |
| C. | f(x)既不是奇函数也不是偶函数,且在(0,+∞)上是增函数 | |
| D. | f(x)既不是奇函数也不是偶函数,且在(0,+∞)上是减函数 |
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{9}=1$ | D. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ |
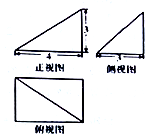
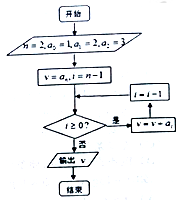
| A. | 48 | B. | 36 | C. | 24 | D. | 12 |
| A. | $-\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\sqrt{3}$ | D. | 2 |
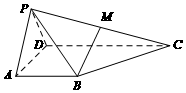 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,$AB=AD=\frac{1}{2}CD$,AB⊥AD,AB∥CD,点M是PC的中点.
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD为等边三角形,$AB=AD=\frac{1}{2}CD$,AB⊥AD,AB∥CD,点M是PC的中点.