题目内容
已知函数f(x)=(x+1)lnx.
(1)指出函数f(x)极值点的个数,并给出证明;
(2)若关于x的不等式mf(x)>2(x-1)对于所有x∈(1,+∞)都成立,求实数m的取值.
(1)指出函数f(x)极值点的个数,并给出证明;
(2)若关于x的不等式mf(x)>2(x-1)对于所有x∈(1,+∞)都成立,求实数m的取值.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)利用导数求函数的极值,结合图象即可得出结论;
(2)利用(1)的结论,利用导数把恒成立问题转化为求函数最值问题解决.
(2)利用(1)的结论,利用导数把恒成立问题转化为求函数最值问题解决.
解答:
解:(1)f′(x)=lnx+
=
=0,∴xlnx+x+1=0即lnx=-1-
,
作出y=lnx与y=-1-
的图象如图,可知两图象只有一个交点,
∴f′(x)=0,只有一个根,函数f(x)只有一个极值点.
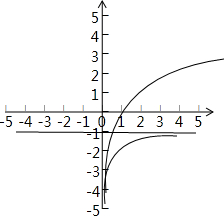
(2)mf(x)>2(x-1)对于所有x∈(1,+∞)都成立,
∴m(x+1)lnx-2(x-1)>0,对于所有x∈(1,+∞)都成立,
即mxlnx+mlnx-2x+2>0,对于所有x∈(1,+∞)都成立,
令g(x)=mxlnx+mlnx-2x+2则g′(x)=m•
-2=mf′(x)-2,
由(1)知当x>1时,f′(x)>2,
又g(0)=0,
∴要使mxlnx+mlnx-2x+2>0,对于所有x∈(1,+∞)都成立,
只要使g(x)在(1,+∞)上单调递增即可,
即g′(x)=m•
-2=mf′(x)-2>0即m>
,
∵(
)max=1,
∴m>1.
∴实数m的取值是(1,+∞)
| x+1 |
| x |
| xlnx+x+1 |
| x |
| 1 |
| x |
作出y=lnx与y=-1-
| 1 |
| x |
∴f′(x)=0,只有一个根,函数f(x)只有一个极值点.
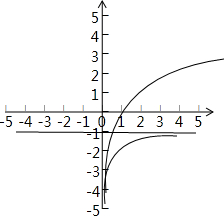
(2)mf(x)>2(x-1)对于所有x∈(1,+∞)都成立,
∴m(x+1)lnx-2(x-1)>0,对于所有x∈(1,+∞)都成立,
即mxlnx+mlnx-2x+2>0,对于所有x∈(1,+∞)都成立,
令g(x)=mxlnx+mlnx-2x+2则g′(x)=m•
| xlnx+x+1 |
| x |
由(1)知当x>1时,f′(x)>2,
又g(0)=0,
∴要使mxlnx+mlnx-2x+2>0,对于所有x∈(1,+∞)都成立,
只要使g(x)在(1,+∞)上单调递增即可,
即g′(x)=m•
| xlnx+x+1 |
| x |
| 2 |
| f′(x) |
∵(
| 2 |
| f′(x) |
∴m>1.
∴实数m的取值是(1,+∞)
点评:本题主要考查利用导数判断函数单调性求极值最值问题,考查学生数形结合思想及和成立问题的等价转化能力和运算求解能力,属于难题.

练习册系列答案
相关题目
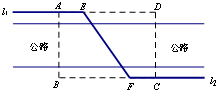 如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB=60m,BC=80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=