题目内容
解不等式：loga
＞logax（a＞0且a≠1）．
| 2x+3 |
考点：指、对数不等式的解法
专题：函数的性质及应用,不等式的解法及应用
分析：本题先对对数函数的底数进行分类讨论，根据不同的单调性去对数符号，得到代数不等式，再解相应的不等式组，得到本题的结论．
解答：
解：当a＞1时，
原不等式转化为：
，
解得：0＜x＜3，此时原不等式的解集为{x|0＜x＜3}；
当0＜a＜1时，原不等式转化为：
，
解得：x＞3，此时原不等式的解集为{x|x＞3}．
综上，当a＞1时，原不等式的解集为{x|0＜x＜3}；
当0＜a＜1时，原不等式的解集为{x|x＞3}．
原不等式转化为：
|
解得：0＜x＜3，此时原不等式的解集为{x|0＜x＜3}；
当0＜a＜1时，原不等式转化为：
|
解得：x＞3，此时原不等式的解集为{x|x＞3}．
综上，当a＞1时，原不等式的解集为{x|0＜x＜3}；
当0＜a＜1时，原不等式的解集为{x|x＞3}．
点评：本题考查了对数函数的单调性和定义域，还考查了分类讨论和化归转化的数学思想方法，本题难度适中，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
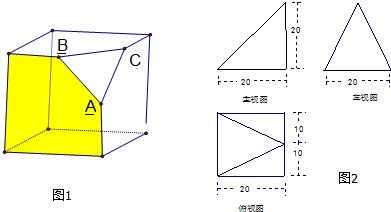
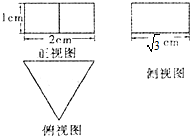某个几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的表面积是（ ）A、
| ||
B、6+
| ||
C、6+2
| ||
D、6+3
|