题目内容
以下是关于函数f(x)=
的四个命题:
①f(x)的图象关于y轴对称;
②f(x)在区间[-1,0]∪[1,+∞)上单调递减;
③f(x)在x=-1处取得极小值,在x=1处取得极大值;
④f(x)有最大值,无最小值;
⑤若方程f(x)-k=0至少有三个不同的实根,则实数k的取值范围是(0,2).
其中为真命题的是 (请填写你认为是真命题的序号).
| 4|x| |
| x2+1 |
①f(x)的图象关于y轴对称;
②f(x)在区间[-1,0]∪[1,+∞)上单调递减;
③f(x)在x=-1处取得极小值,在x=1处取得极大值;
④f(x)有最大值,无最小值;
⑤若方程f(x)-k=0至少有三个不同的实根,则实数k的取值范围是(0,2).
其中为真命题的是
考点:根的存在性及根的个数判断,函数的图象
专题:函数的性质及应用
分析:先求出函数的对称性,单调性,画出函数的草图,从而得出答案.
解答:
解:①定义域关于原点对称,f(-x)=f(x),f(x)的图象关于y轴对称,故①正确;
②x>0时,f(x)=
,f′(x)=
,令f′(x)≤0,解得:x>1,∴f(x)在[1,+∞)递减,
x≤0时,f(x)=
,f′(x)=
,令f′(x)≤0,解得:-1≤x≤0,∴f(x)在[-1,0]递减,
画出函数f(x)的草图:

∴f(x)分别在区间[-1,0]和[1,+∞)上单调递减,故②错误;
③f(x)在x=-1处取得极大值,在x=1处取得极大值,故③错误;
④由②中的图象得:④正确;
⑤由②中的图象得:⑤正确;
故答案为:①④⑤.
②x>0时,f(x)=
| 4x |
| x2+1 |
| -4x2+4 |
| (x2+1)2 |
x≤0时,f(x)=
| -4x |
| x2+1 |
| 4x2-4 |
| (x2+1)2 |
画出函数f(x)的草图:

∴f(x)分别在区间[-1,0]和[1,+∞)上单调递减,故②错误;
③f(x)在x=-1处取得极大值,在x=1处取得极大值,故③错误;
④由②中的图象得:④正确;
⑤由②中的图象得:⑤正确;
故答案为:①④⑤.
点评:本题考查了函数的单调性,函数的极值问题,是一道中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
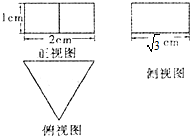 某个几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的表面积是( )
某个几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的表面积是( )A、
| ||
B、6+
| ||
C、6+2
| ||
D、6+3
|