题目内容
设xa=yb=zc.且
+
=
,求证:z=xy.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:设xa=yb=zc=k>0,则a=
,b=
,c=
.代入
+
=
,即可得出.
| lgk |
| lgx |
| lgk |
| lgy |
| lgk |
| lgz |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
解答:
证明:设xa=yb=zc=k>0,则a=
,b=
,c=
.
∵
+
=
,∴
+
=
.
∴lg(xy)=lgz,
∴z=xy.
| lgk |
| lgx |
| lgk |
| lgy |
| lgk |
| lgz |
∵
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| lgx |
| lgk |
| lgy |
| lgk |
| lgz |
| lgk |
∴lg(xy)=lgz,
∴z=xy.
点评:本题考查了对数的运算性质,属于基础题.

练习册系列答案
相关题目
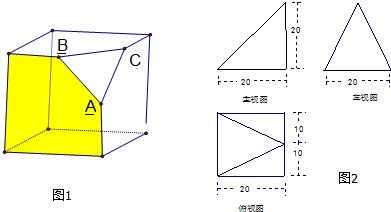
已知△ABC是边长为2的正三角形,则它的平面直观图△A′B′C′的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
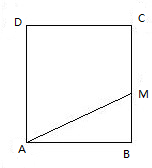 已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.
已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.