题目内容
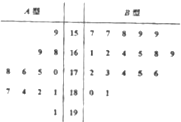 某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”
某工厂随机抽取处12件A型产品和18件B型产品,将这30件产品的尺寸编成如图所示的茎叶图(单位:cm),若尺寸在175cm以上(包括175cm)的产品定义为“标准件”,尺寸在175cm以下(不包括175cm)的产品定义为“非标准件”(1)如果用分层抽样的方法从这30件“标准件”和“非标准件”中选取5件,求出这5件产品中“标准件”和“非标准件”的件数;
(2)从(1)中抽出的5件中抽取2件,那么至少有一件是“标准件”的概率是多少?
考点:古典概型及其概率计算公式,分层抽样方法,茎叶图
专题:概率与统计
分析:(1)按分层抽样抽取5件,这5件中,“标准件”的个数为5×
=2,“非标准件”的个数为5×
=3,
(2)设事件A=“从2件标准件和3件非标准件中选2件,至少有一件是标准件”,则
=“从2件标准件和3件非标准件中选2件,全是非标准件”,利用对立事件的概率公式,可求至少有一件是“标准件”的概率;
| 12 |
| 30 |
| 12 |
| 30 |
(2)设事件A=“从2件标准件和3件非标准件中选2件,至少有一件是标准件”,则
. |
| A |
解答:
解:(1)读取茎叶图中数据,“标准件”的个数为12,“非标准件”的个数为18
按分层抽样抽取5件,这5件中,“标准件”的个数为5×
=2,“非标准件”的个数为5×
=3
(2)设事件A=“从2件标准件和3件非标准件中选2件,至少有一件是标准件”,
则
=“从2件标准件和3件非标准件中选2件,全是非标准件”,
∵从2件标准件和3件非标准件中选2件共有
=10种不同情况,
其中全是非标准件有
=3种不同情况,
∴P(
)=
,
则P(A)=1-P(
)=1-
=
,
答:至少有一件是“标准件”的概率是
.
按分层抽样抽取5件,这5件中,“标准件”的个数为5×
| 12 |
| 30 |
| 12 |
| 30 |
(2)设事件A=“从2件标准件和3件非标准件中选2件,至少有一件是标准件”,
则
. |
| A |
∵从2件标准件和3件非标准件中选2件共有
| C | 2 5 |
其中全是非标准件有
| C | 2 3 |
∴P(
. |
| A |
| 3 |
| 10 |
则P(A)=1-P(
. |
| A |
| 3 |
| 10 |
| 7 |
| 10 |
答:至少有一件是“标准件”的概率是
| 7 |
| 10 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
相关题目
若A,B是一次试验的两个事件,则“事件A,B对立”是“事件A,B互斥”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |